题目内容
17．用一条直线将一个菱形分割成两个多边形，若这两个多边形的内角和分别为M和N，则M+N的值不可能是（ ）
| A． | 360° | B． | 540° | C． | 630° | D． | 720° |
分析 如图，一条直线将该菱形ABCD分割成两个多边形（含三角形）的情况有以上三种，分别求出每一个图形的两个多边形的内角和即可作出判断．
解答 解：如图，一条直线将该菱形ABCD分割成两个多边（含三角形）的情况有以上三种，
①当直线不经过任何一个原来菱形的顶点，
此时菱形分割为一个五边形和三角形，
∴M+N=540°+180°=720°；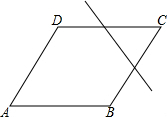
②当直线经过一个原来菱形的顶点，
此时菱形分割为一个四边形和一个三角形，
∴M+N=360°+180°=540°；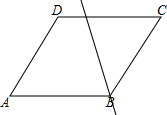
③当直线经过两个原来菱形的对角线顶点，
此时菱形分割为两个三角形，
∴M+N=180°+180°=360°．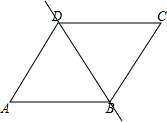
．
故选：C．
点评 此题考查了分类讨论的思想，解题关键是分类讨论，每一个图形都要利用多边形的内角和公式．
练习册系列答案
名校课堂系列答案
相关题目
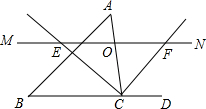如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．
5．
老北京的老行当中有一行叫做“抓彩卖糖”：商贩将高丽纸裁成许多小条，用矾水在上面写上糖的块数，最少一块，多的是三块或五块，再将枝条混合在一起．游戏时叫儿童随意抽取一张，然后放入水罐中浸湿，即出现白道儿，按照上面的白道儿数给糖．一个商贩准备了10张质地均匀的纸条，其中能得到一块糖的纸条有5张，能得到三块塘的纸条有3张，能得到五块糖的纸条有2张．从中随机抽取一张纸条，恰好是能得到三块塘的纸条的概率是（ ）
老北京的老行当中有一行叫做“抓彩卖糖”：商贩将高丽纸裁成许多小条，用矾水在上面写上糖的块数，最少一块，多的是三块或五块，再将枝条混合在一起．游戏时叫儿童随意抽取一张，然后放入水罐中浸湿，即出现白道儿，按照上面的白道儿数给糖．一个商贩准备了10张质地均匀的纸条，其中能得到一块糖的纸条有5张，能得到三块塘的纸条有3张，能得到五块糖的纸条有2张．从中随机抽取一张纸条，恰好是能得到三块塘的纸条的概率是（ ）| A． | $\frac{1}{10}$ | B． | $\frac{3}{10}$ | C． | $\frac{1}{5}$ | D． | $\frac{1}{2}$ |
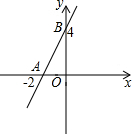如图，直线y=kx+b交坐标轴于A，B两点，则不等式kx+b≤0的解集在数轴上表示正确的是（ ）
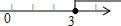
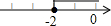
如图，若AB=CD，AE=DF，CE=BF，则AB与CD平行吗？为什么？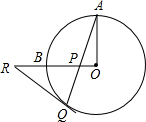
如图，OA、OB是⊙O的两条互相垂直的半径，P为OB上任一点，AP的延长线交⊙O于点Q，过点Q作⊙O的切线交OB的延长线于点R，求证：RP=RQ．