题目内容
10．一次函数y=2x-3+b中，y随着x的增大而增大，当b=3时，函数图象经过原点．分析 根据一次函数的性质k＞0，y随x的增大而增大，函数从左到右上升；k＜0，y随x的增大而减小，函数从左到右下降可直接得到答案．
解答 解：一次函数y=2x-3+b中，
∵k=2＞0，
∴y随着x的增大而增大，
∵函数的图象过原点，
∴-3+b=0，
解得：b=3，
当b=3时，函数图象经过原点．
故答案为：增大，b=3；
点评 本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
20．如果10b=n，那么b为n的劳格数，记为b=d（n），由定义可知：10b=n与b=d（n）所表示的b、n两个量之间的同一关系．
（1）根据劳格数的定义，填空：d（10）=1，d（102）=2．
那么：d（103）=3，d（10-2）=-2
（2）劳格数有如下运算性质：
若m、n为正数，则d（mn）=d（m）+d（n），d（ $\frac{m}{n}$）=d（m）-d（n）．
根据运算性质，填空：
$\frac{d（{a}^{3}）}{d（a）}$=2d（a）（a为正数）．
若d（3）=0.4771，则d（9）=0.9542，d（$\frac{3}{10}$）=-0.5229；
（3）如表中与数x对应的劳格数d（x）有且只有两个是错误的，请找出错误的劳格数，说明理由并改正．
（1）根据劳格数的定义，填空：d（10）=1，d（102）=2．
那么：d（103）=3，d（10-2）=-2
（2）劳格数有如下运算性质：
若m、n为正数，则d（mn）=d（m）+d（n），d（ $\frac{m}{n}$）=d（m）-d（n）．
根据运算性质，填空：
$\frac{d（{a}^{3}）}{d（a）}$=2d（a）（a为正数）．
若d（3）=0.4771，则d（9）=0.9542，d（$\frac{3}{10}$）=-0.5229；
（3）如表中与数x对应的劳格数d（x）有且只有两个是错误的，请找出错误的劳格数，说明理由并改正．
| x | 0.8 | 2 | 3.2 | 4 | 5 | 8 |
| d（x） | 6a-3b+1 | 2a-b | 10a-5b | 4a-2b | 1-2a+b | 6a-3b |
如图，在△ABC中，AB=AC，∠ABC、∠ACB的平分线BD，CE相交于O点，且BD交AC于点D，CE交AB于点E，某同学分析图形后得出以下结论，上述结论一定正确的是①③④（填代号）．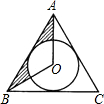
如图，已知正△ABC的边长为9，⊙O是它的内切圆，则图中阴影部分的面积为$\frac{27\sqrt{3}-9π}{4}$．（结果保留π）
如图，AB=AC，AC的垂直平分线DE交AB于D，交AC于E，BC=6，△CDB的周长为15，求AC．