题目内容
8.解分式方程:(1)$\frac{1}{x-2}$=$\frac{4}{{x}^{2}-4}$
(2)$\frac{{x}^{2}-4x}{{x}^{2}-1}$+1=$\frac{2x}{x+1}$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:x+2=4,
解得:x=2,
经检验x=2是增根,分式方程无解;
(2)去分母得:x2-4x+x2-1=2x2-2x,
解得:x=-$\frac{1}{2}$,
经检验x=-$\frac{1}{2}$是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
2.当x=( )时,|x+6|有最( )值,是( )
| A. | 0,大,0 | B. | 0,小,0 | C. | -6,大,0 | D. | -6,小,0 |
17.在-8,2.6,-3$\frac{1}{2}$,2$\frac{2}{3}$,-5.7中,负分数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 5个 |
 如图,已知点O在直线AB上,0D、0E分别平分∠BOC、∠AOC,∠BOC=80°.
如图,已知点O在直线AB上,0D、0E分别平分∠BOC、∠AOC,∠BOC=80°.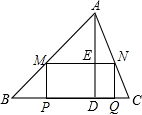 在锐角△ABC中,BC=6,S△ABC=12,矩形MPQN的两个顶点M,N分别在AB,AC上,另两个顶点P,Q均在BC上,高AD交MN于点E,设MN的长为x,矩形MPQN的面积为y.
在锐角△ABC中,BC=6,S△ABC=12,矩形MPQN的两个顶点M,N分别在AB,AC上,另两个顶点P,Q均在BC上,高AD交MN于点E,设MN的长为x,矩形MPQN的面积为y. 如图,在一面靠墙的空地上,用长为24米的篱笆,围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x(m),面积为S(m2).
如图,在一面靠墙的空地上,用长为24米的篱笆,围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x(m),面积为S(m2).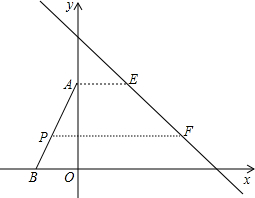 如图,△ABO的顶点A、B的坐标分别为(0,4)、(-2,0),直线l交x轴于C、交y轴于D,且它所对应的函数表达式为y=-x+6;规定:对于平面上的某一点M,当它沿水平向右的方向平移,平移到直线l上为止,这个过程中平移的距离,称为点M的“右平移距离”.
如图,△ABO的顶点A、B的坐标分别为(0,4)、(-2,0),直线l交x轴于C、交y轴于D,且它所对应的函数表达式为y=-x+6;规定:对于平面上的某一点M,当它沿水平向右的方向平移,平移到直线l上为止,这个过程中平移的距离,称为点M的“右平移距离”.