题目内容
10. 已知:∠1=∠2,∠B=∠C,AB=AC,求证:AD=AE,∠D=∠E.
已知:∠1=∠2,∠B=∠C,AB=AC,求证:AD=AE,∠D=∠E.
分析 先求出∠BAE=∠CAD,再利用“角边角”证明△ABE和△ACD全等,根据全等三角形对应边相等,全等三角形对应角相等证明即可.
解答 证明:∵∠1=∠2,
∴∠2+∠BAC=∠1+∠BAC,
即∠BAE=∠CAD,
在△ABE和△ACD中,$\left\{\begin{array}{l}{∠BAE=∠CAD}\\{AB=AC}\\{∠B=∠C}\end{array}\right.$,
∴△ABE≌△ACD(ASA),
∴AD=AE,∠D=∠E.
点评 本题考查了全等三角形的判定与性质,熟练掌握三角形全等的判定方法是解题的关键,易错点是求出∠BAE=∠CAD.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
2. 如图,若输入x的值为-5,则输出的结果为( )
如图,若输入x的值为-5,则输出的结果为( )
 如图,若输入x的值为-5,则输出的结果为( )
如图,若输入x的值为-5,则输出的结果为( )| A. | -6 | B. | -5 | C. | 5 | D. | 6 |
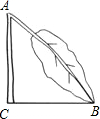 一棵树因雪灾于A处折断,如图所示,测得树梢触地点B到树根C处的距离为4米,∠ABC约45°,树干AC垂直于地面,那么此树在未折断之前的高度约为(4+4$\sqrt{2}$)米(答案可保留根号)
一棵树因雪灾于A处折断,如图所示,测得树梢触地点B到树根C处的距离为4米,∠ABC约45°,树干AC垂直于地面,那么此树在未折断之前的高度约为(4+4$\sqrt{2}$)米(答案可保留根号) 如图是一套住房的平面图,尺寸如图所.
如图是一套住房的平面图,尺寸如图所. 如图大正方形的面积为a2(a>0),小正方形的面积为b2(b>0),求阴影部分的面积.
如图大正方形的面积为a2(a>0),小正方形的面积为b2(b>0),求阴影部分的面积.