题目内容
 如图,平面直角坐标系中A(-1,0),B(3,0),现同时将A、B分别向上平移2个单位,再向右平移1个单位,分别得到A、B的对应点C、D,连接AC、BD
如图,平面直角坐标系中A(-1,0),B(3,0),现同时将A、B分别向上平移2个单位,再向右平移1个单位,分别得到A、B的对应点C、D,连接AC、BD(1)直接写出C、D的坐标:C
(2)在y轴负半轴上是否存在点M,连接MA、MB使得S△MAB>S四边形ABCD?若存在,求出M点纵坐标的取值范围;若不存在说明理由
(3)点P为线段BD上一动点,连PC、PO,当点P在BD上移动(不含端点)现给出①
| ∠DCP+∠BOP |
| ∠CPO |
| ∠DCP+∠CPO |
| ∠BOP |
其中有且只有一个正确,请你找出这个结论并求其值.
考点:坐标与图形性质,平行线的性质,三角形的面积,坐标与图形变化-平移
专题:
分析:(1)根据向右平移横坐标加,向上平移纵坐标加写出点C、D的坐标即可,再根据平行四边形的面积公式列式计算即可得解;
(2)根据三角形的面积求出S△MAB=S四边形ABCD时点M到AB的距离,再写出M的纵坐标的取值范围即可;
(3)过点P作PE∥CD,根据两直线平行,内错角相等可得∠DCP=∠CPE,根据平行公理可得PE∥AB,再根据两直线平行,内错角相等可得∠BOP=∠OPE,然后求出∠DCP+∠BOP=∠CPE+∠OPE=∠CPO,再求出比值即可.
(2)根据三角形的面积求出S△MAB=S四边形ABCD时点M到AB的距离,再写出M的纵坐标的取值范围即可;
(3)过点P作PE∥CD,根据两直线平行,内错角相等可得∠DCP=∠CPE,根据平行公理可得PE∥AB,再根据两直线平行,内错角相等可得∠BOP=∠OPE,然后求出∠DCP+∠BOP=∠CPE+∠OPE=∠CPO,再求出比值即可.
解答:解:(1)C(0,2),D(4,2),
四边形ABCD的面积=(3+1)×2=8;
(2)设S△MAB=S四边形ABCD时点M到AB的距离为h,
则
×(3+1)h=8,
解得h=4,
∵点M在y轴的负半轴,
∴要使S△MAB>S四边形ABCD,则M点纵坐标的取值范围y<-4;
(3)过点P作PE∥CD,
则∠DCP=∠CPE,
∵AB∥CD,
∴PE∥AB,
∴∠BOP=∠OPE,
∴∠DCP+∠BOP=∠CPE+∠OPE=∠CPO,
∴
=1,值不变.
四边形ABCD的面积=(3+1)×2=8;
(2)设S△MAB=S四边形ABCD时点M到AB的距离为h,
则
| 1 |
| 2 |
解得h=4,
∵点M在y轴的负半轴,
∴要使S△MAB>S四边形ABCD,则M点纵坐标的取值范围y<-4;

(3)过点P作PE∥CD,
则∠DCP=∠CPE,
∵AB∥CD,
∴PE∥AB,
∴∠BOP=∠OPE,
∴∠DCP+∠BOP=∠CPE+∠OPE=∠CPO,
∴
| ∠DCP+∠BOP |
| ∠CPO |
点评:本题考查了坐标与图形性质,平行线的性质,三角形的面积,坐标与图形变化-平移,熟记各性质是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,∠A=150°,AB=20cm,AC=30cm,则△ABC的面积为( )
如图,在△ABC中,∠A=150°,AB=20cm,AC=30cm,则△ABC的面积为( )| A、330cm2 |
| B、450cm2 |
| C、150cm2 |
| D、300cm2 |
坐标平面上的点P(20,-10)向上平移20个单位,再向左平移10个单位后,点P的坐标变为( )
| A、(20,10) |
| B、(-20,10) |
| C、(10,10) |
| D、(40,-20) |
已知方程组
,且-1<x-y<0,则m的取值范围是( )
|
A、-1<m<-
| ||
B、0<m<
| ||
| C、0<m<1 | ||
D、
|
 如图,EF∥AD,∠1=∠2,求证DG∥AB的过程填写完整.
如图,EF∥AD,∠1=∠2,求证DG∥AB的过程填写完整.
 已知如图,在菱形ABCD中,CO⊥BD,垂足为点O,E为BC上一点,F为AD延长线上一点,EF交CD于点G,EG=FG=DG,连接OE、OF.
已知如图,在菱形ABCD中,CO⊥BD,垂足为点O,E为BC上一点,F为AD延长线上一点,EF交CD于点G,EG=FG=DG,连接OE、OF.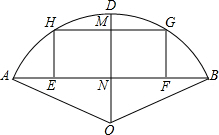 已知,如图,以O为圆心,OA为半径画弧,∠AOB=120°,弓形高ND=4厘米,矩形EFGH的两顶点E,F在弦AB上,H,G在
已知,如图,以O为圆心,OA为半径画弧,∠AOB=120°,弓形高ND=4厘米,矩形EFGH的两顶点E,F在弦AB上,H,G在