题目内容
8.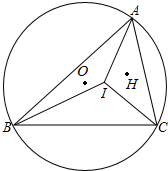 锐角△ABC中,AB>BC>CA,O、I、H分别是它的外心、内心,垂心,已知∠A=60°,求证:(1)∠OIH-∠ABC是一个定值;(2)∠OIH+∠ACB也是一个定值.
锐角△ABC中,AB>BC>CA,O、I、H分别是它的外心、内心,垂心,已知∠A=60°,求证:(1)∠OIH-∠ABC是一个定值;(2)∠OIH+∠ACB也是一个定值.
分析 (1)连接BH并延长交AC于E,连接CH并延长交AB于F,作OD⊥AB于D,连接OB、OC、OI、IH,设∠CBE=α,则∠ACB=90°-α,由圆周角定理得出∠BOD=∠ACB=∠BCE,得出∠ABO=∠OBD=∠CBE=α,∠ABC=∠ABE+α=(90°-∠A)+α=30°+α,证出∠BOC=∠BIC=∠BHC,得出B、O、I、H、C五点共圆,得出∠OBC=∠OCB=30°,∠CIH=∠CBH=α,∠OIC=180°-∠OBC=150°,得出∠OIH=150°+α,即可得出结论;
(2)∠OIH+∠ACB=(150°+α)+(90°-α)=240°,即可得出结论.
解答 证明:(1)连接BH并延长交AC于E,连接CH并延长交AB于F,作OD⊥AB于D,连接OB、OC、OI、IH,如图所示:
设∠CBE=α,则∠ACB=90°-α,
由圆周角定理得:∠BOD=∠ACB=∠BCE,
∴∠ABO=∠OBD=∠CBE=α,∠ABC=∠ABE+α=(90°-∠A)+α=30°+α,
∵∠BOC=2∠BAC=120°,∠BIC=90°+$\frac{1}{2}$∠BAC=120°,∠BHC=∠EHF=180°-∠A=120°,
∴∠BOC=∠BIC=∠BHC,
∴B、O、I、H、C五点共圆,
∴∠OBC=∠OCB=30°,∠CIH=∠CBH=α,∠OIC=180°-∠OBC=150°,
∴∠OIH=150°+α,
∴∠OIH-∠ABC=(150°+α)-(30°+α)=120°,
∴∠OIH-∠ABC是一个定值;
(2)∠OIH+∠ACB=(150°+α)+(90°-α)=240°,
∴∠OIH+∠ACB也是一个定值.
点评 本题考查了三角形的外心、内心、垂心、圆周角定理、五点共圆、垂径定理等知识;本题综合性强,难度较大,特别是(1)中,需要通过作多条辅助线证明五点共圆才能得出结果.

甲超市:
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 5 | 10 | 5 |
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 10 | 5 | 10 |

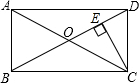 如图,在矩形ABCD中,BC=12,对角线AC与BD相交于点O,CE⊥BD于点E,BE=3ED.求CE的长.
如图,在矩形ABCD中,BC=12,对角线AC与BD相交于点O,CE⊥BD于点E,BE=3ED.求CE的长.