题目内容
17.已知直线y1=k1x+b1经过原点和点(-2,-4),直线y2=k2x+b2经过点(1,5)和点(8,-2),求:(1)y1和y的函数关系式,并在同一坐标系中画出函数图象;
(2)若两直线交于点M,求M的坐标;
(3)若直线y2与x轴交于点N,试求三角形MON的面积.
分析 (1)本题中,因为直线y1=k1x+b1经过原点和点(-2,-4),直线y2=k2x+b2经过点(8,-2)和点(1,5),所以可分别求出两直线的解析式y1=2x,y2=-x+6,
(2)在(1)中,把两解析式联立,得到方程组,解之即可求得两直线交点M的坐标;
(2)因为直线y2与x轴交于点N(6,0),所以可求出△MON的面积.
解答 解:(1)∵直线y1=k1x+b1经过原点和点(-2,-4),直线y2=k2x+b2经过点(8,-2)和点(1,5),
∴$\left\{\begin{array}{l}{{b}_{1}=0}\\{-4=-2{k}_{1}}\end{array}\right.$和$\left\{\begin{array}{l}{-2=8{k}_{2}+{b}_{2}}\\{5={k}_{2}+{b}_{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{k}_{1}=2}\\{{b}_{1}=0}\end{array}\right.$和$\left\{\begin{array}{l}{{k}_{2}=-1}\\{{b}_{2}=6}\end{array}\right.$,
∴y1=2x,y2=-x+6,
图象如图:
(2)∵y1=2x,y2=-x+6,且两直线相交于M,
∴$\left\{\begin{array}{l}{y=2x}\\{y=-x+6}\end{array}\right.$解之得$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$,
即点M的坐标为(2,4).
(3)∵直线y2与x轴交于点N,
∴N(6,0),
∴△MON的面积=$\frac{1}{2}$×6×4=12
点评 此题考查两直线相交问题,解决此类题目的关键是灵活运用待定系数法求函数的解析式,并能结合方程组求交点坐标,进而利用图象求相应图象的面积.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 7x2+5y | B. | -7x2-5y | C. | -7x2+5y | D. | 7x2-5y |
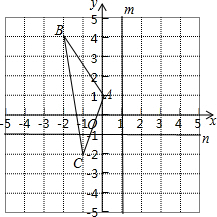 在平面直角坐标系中,A(0,1),B(-2,4),C(-1,-2),试分别作出△ABC关于直线m:x=1和直线n:y=-1的对称图形,并写出对应顶点的坐标.
在平面直角坐标系中,A(0,1),B(-2,4),C(-1,-2),试分别作出△ABC关于直线m:x=1和直线n:y=-1的对称图形,并写出对应顶点的坐标.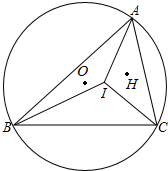 锐角△ABC中,AB>BC>CA,O、I、H分别是它的外心、内心,垂心,已知∠A=60°,求证:(1)∠OIH-∠ABC是一个定值;(2)∠OIH+∠ACB也是一个定值.
锐角△ABC中,AB>BC>CA,O、I、H分别是它的外心、内心,垂心,已知∠A=60°,求证:(1)∠OIH-∠ABC是一个定值;(2)∠OIH+∠ACB也是一个定值. 在同一直角坐标系内分别作出一次函数y=5-x和y=2x-1的图象,这两个图象有交点吗?如果有请你结合图象直接写出交点的坐标?
在同一直角坐标系内分别作出一次函数y=5-x和y=2x-1的图象,这两个图象有交点吗?如果有请你结合图象直接写出交点的坐标? 如图所示,在等腰梯形ABCD中,AB∥CD,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积是18cm2.
如图所示,在等腰梯形ABCD中,AB∥CD,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积是18cm2.