题目内容
8.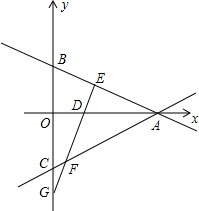 如图,在平面直角坐标系中,一直线分别与坐标轴交于A(a,0)、B(0,b)两点,满足$\sqrt{(a-3)^{2}}$+|b-1|=0,在y轴负半轴上截取OC=OB.
如图,在平面直角坐标系中,一直线分别与坐标轴交于A(a,0)、B(0,b)两点,满足$\sqrt{(a-3)^{2}}$+|b-1|=0,在y轴负半轴上截取OC=OB.(1)求直线AC的解析式;
(2)在x轴上取一点D(1,0),过D作DE⊥AB于E,交AC于F,交y轴于G,求F点的坐标.
分析 (1)首先根据$\sqrt{(a-3)^{2}}$+|b-1|=0,可得$\sqrt{(a-3)^{2}}$=0,且|b-1|=0,据此求出a,b的值各是多少;然后根据OC=OB,求出C的坐标,即可求出直线AC的解析式.
(2)首先根据DE⊥AB,求出直线DE的斜率,进而求出直线DE的解析式是多少;然后联立直线DE、AC的解析式,求出F点的坐标是多少即可.
解答 解:(1)∵$\sqrt{(a-3)^{2}}$+|b-1|=0,
∴$\sqrt{(a-3)^{2}}$=0,且|b-1|=0,
∴a-3=0,且b-1=0,
解得a=3,b=1,
∴A(3,0)、B(0,1),
∵OC=OB,
∴C(0,-1),
设直线AC的解析式是y=mx+n,
则$\left\{\begin{array}{l}{3m+n=0}\\{n=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=\frac{1}{3}}\\{n=-1}\end{array}\right.$.
∴直线AC的解析式是y=$\frac{1}{3}$x-1.
(2)∵A(3,0)、B(0,1),
∴直线AB的斜率是:
k=$\frac{1-0}{0-3}$=-$\frac{1}{3}$,
∵DE⊥AB,
∴直线DE的斜率是:
k′=(-1)÷(-$\frac{1}{3}$)=3,
∵点D的坐标是(1,0),
∴直线DE的解析式是y=3(x-1)=3x-3,
联立$\left\{\begin{array}{l}{y=3x-3}\\{y=\frac{1}{3}x-1}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=\frac{3}{4}}\\{y=-\frac{3}{4}}\end{array}\right.$.
∴F点的坐标是($\frac{3}{4}$,-$\frac{3}{4}$).
点评 (1)此题主要考查了一次函数综合题,分析推理能力,数形结合思想的应用,从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了直线解析式的求法,要熟练掌握.

 已知,如图,C为线段AB上除端点外的任意一点,AD∥BE,且∠D=∠1,∠E=∠2.求∠DCE的度数.
已知,如图,C为线段AB上除端点外的任意一点,AD∥BE,且∠D=∠1,∠E=∠2.求∠DCE的度数.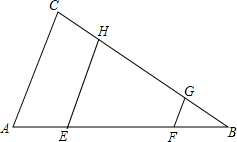 如图,在△ABC中,AE=BF,EH∥AC,FG∥AC,线段EH,FG,AC之间有怎样的数量关系?证明你的结论.
如图,在△ABC中,AE=BF,EH∥AC,FG∥AC,线段EH,FG,AC之间有怎样的数量关系?证明你的结论. 已知点A(-4,a),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0,x<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
已知点A(-4,a),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0,x<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.