题目内容
已知,点P是△ABC内任意一点,连接AP,BP,证明:AC+BC>AP+BP.
考点:三角形三边关系
专题:证明题
分析:延长AP,交BC于D.在△ACD中,根据三角形两边之和大于第三边可得AC+CD>AP+PD,同理在△PBD中,可得PD+DB>BP,再根据不等式的性质得到AC+CD+PD+DB>AP+PD+BP,进而即可证明AC+BC>AP+BP.
解答: 证明:如图,延长AP,交BC于D.
证明:如图,延长AP,交BC于D.
在△ACD中,AC+CD>AP+PD,
在△PBD中,PD+DB>BP,
所以AC+CD+PD+DB>AP+PD+BP,
即AC+BC>AP+BP.
 证明:如图,延长AP,交BC于D.
证明:如图,延长AP,交BC于D.在△ACD中,AC+CD>AP+PD,
在△PBD中,PD+DB>BP,
所以AC+CD+PD+DB>AP+PD+BP,
即AC+BC>AP+BP.
点评:本题考查了三角形三边关系定理:三角形两边之和大于第三边.准确作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
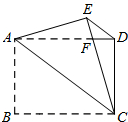 如图,把矩形纸片ABCD沿对角线AC折叠,点B落在点E处,EC与AD相交于点F,若AB=4,BC=6,求△FAC的周长和面积.
如图,把矩形纸片ABCD沿对角线AC折叠,点B落在点E处,EC与AD相交于点F,若AB=4,BC=6,求△FAC的周长和面积.