题目内容
19.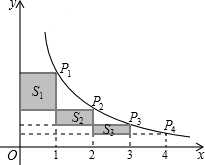 如图,在反比例函数$y=\frac{k}{x}$(x>0)的图象上有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴和y轴的垂线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3,若S1+S2+S3=2.4,则k的值为3.2.
如图,在反比例函数$y=\frac{k}{x}$(x>0)的图象上有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴和y轴的垂线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3,若S1+S2+S3=2.4,则k的值为3.2.
分析 根据反比例函数的几何意义可知图中所构成的阴影部分的面积和正好是从点P1向x轴,y轴引垂线构成的长方形面积减去最下方的长方形的面积,根据S1+S2+S3=2.4列方程求解即可.
解答 解:由题意可知点P1、P2、P3、P4坐标分别为:(1,k),(2,$\frac{k}{2}$,(3,$\frac{k}{3}$),(4,$\frac{k}{4}$).
∴由反比例函数的几何意义可知:S1+S2+S3=[(k-$\frac{k}{2}$)+($\frac{k}{2}$-$\frac{k}{3}$)+($\frac{k}{3}$-$\frac{k}{4}$)]×1
=$\frac{3k}{4}$=2.4,
解得:k=3.2,
故答案为:3.2.
点评 主要考查了反比例函数y=$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,正确理解k的几何意义是解题的关键.

练习册系列答案
相关题目
4.下列根式中,与3$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\sqrt{8}$ | D. | $\sqrt{12}$ |
9.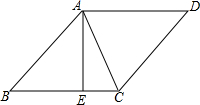 如图,在菱形ABCD中,AB=5,对角线AC=6,过A作AE⊥BC,垂足为E,则AE的长是( )
如图,在菱形ABCD中,AB=5,对角线AC=6,过A作AE⊥BC,垂足为E,则AE的长是( )
 如图,在菱形ABCD中,AB=5,对角线AC=6,过A作AE⊥BC,垂足为E,则AE的长是( )
如图,在菱形ABCD中,AB=5,对角线AC=6,过A作AE⊥BC,垂足为E,则AE的长是( )| A. | 24 | B. | 36 | C. | 48 | D. | 4.8 |
 如图,y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是x>2.
如图,y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是x>2.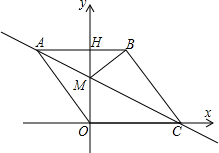 如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.