题目内容
8.在直角坐标系中A(-1,0),B(3,0),C(1,3),以A、B、C、D为顶点的四边形是平行四边形,则点D的坐标为此题答案不唯一,如(-3,3).(写出一个)分析 分别从以AC为对角线,以BC为对角线,以AB为对角线,去分析求解即可求得答案.
解答  解:如图:若以AC为对角线,则点D的坐标为:(-3,3);
解:如图:若以AC为对角线,则点D的坐标为:(-3,3);
若以BC为对角线,则点D的坐标为:(5,3);
若以AB为对角线,则点D的坐标为:(1,-3).
故答案为:此题答案不唯一,如(-3,3).
点评 此题考查了平行四边形的性质.注意利用平移的思想,结合图形求解是关键.

练习册系列答案
相关题目
18.下列等式从左到右的变形,是因式分解的是( )
| A. | a(x-y)=ax-ay | B. | x2-2x+3=x(x-2)+3 | C. | (x-1)(x+4)=x2+3x-4 | D. | x3-2x2+x=x(x-1)2 |
16.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{48}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{4a+12}$ |
3.已知,点A(-6,y1)和点B(1,y2)都在直线y=-$\frac{1}{2}$x-1上,那么y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不确定 |
13.如果线段a,b,c能组成直角三角形,则它们的比可以是( )
| A. | 1:2:4 | B. | 1:3:5 | C. | 6:4:7 | D. | 5:12:13 |
20.若关于x的分式方程$\frac{2}{x-2}$+$\frac{mx}{{x}^{2}-4}$=$\frac{3}{x+2}$有增根,则m的值是( )
| A. | 1 | B. | -4或6 | C. | 6或1 | D. | 1或-4或6 |
18.已知直线y=kx(x≠0)经过点(-1,2),则此正比例函数的解析式为( )
| A. | y=-2x | B. | y=2x | C. | y=-$\frac{1}{2}$x | D. | y=$\frac{1}{2}$x |
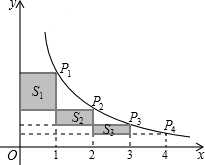 如图,在反比例函数$y=\frac{k}{x}$(x>0)的图象上有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴和y轴的垂线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3,若S1+S2+S3=2.4,则k的值为3.2.
如图,在反比例函数$y=\frac{k}{x}$(x>0)的图象上有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴和y轴的垂线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3,若S1+S2+S3=2.4,则k的值为3.2.