题目内容
7. 如图,y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是x>2.
如图,y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是x>2.
分析 首先根据图象可知,该一次函数y=kx+b的图象经过点(2,0)、(0,-3).因此可确定该一次函数的解析式为y=$\frac{3}{2}$x-3.由于y>0,根据一次函数的单调性,那么x的取值范围即可确定.
解答 解:由图象可知一次函数y=kx+b的图象经过点(2,0)、(0,-3).
∴可列出方程组 $\left\{\begin{array}{l}{2k+b=0}\\{b=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=-3}\end{array}\right.$,
∴该一次函数的解析式为y=$\frac{3}{2}$x-3,
∴当y>0时,x的取值范围是:x>2.
故答案为:x>2
点评 本题主要考查了一次函数的图象性质,要掌握一次函数的单调性以及x、y交点坐标的特殊性才能灵活解题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
18.下列等式从左到右的变形,是因式分解的是( )
| A. | a(x-y)=ax-ay | B. | x2-2x+3=x(x-2)+3 | C. | (x-1)(x+4)=x2+3x-4 | D. | x3-2x2+x=x(x-1)2 |
15.若a>b,则下列不等式中成立的是( )
| A. | a+3<b+3 | B. | a-3<b-3 | C. | 3a<3b | D. | -3a<-3b |
16.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{48}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{4a+12}$ |
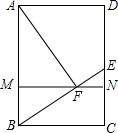 如图,已知矩形ABCD中,点E是CD边上的一点,连结BE,过点A作AF⊥BE.垂足为点F,且AF=BE,过点F作MN∥BC,与AB、CD边分别交于点M、N,求证:四边形AMND为正方形.
如图,已知矩形ABCD中,点E是CD边上的一点,连结BE,过点A作AF⊥BE.垂足为点F,且AF=BE,过点F作MN∥BC,与AB、CD边分别交于点M、N,求证:四边形AMND为正方形.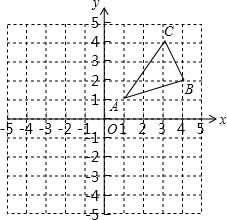 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4) 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示.
甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示.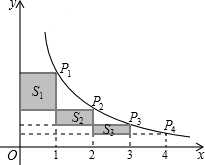 如图,在反比例函数$y=\frac{k}{x}$(x>0)的图象上有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴和y轴的垂线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3,若S1+S2+S3=2.4,则k的值为3.2.
如图,在反比例函数$y=\frac{k}{x}$(x>0)的图象上有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴和y轴的垂线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3,若S1+S2+S3=2.4,则k的值为3.2.