题目内容
4.下列根式中,与3$\sqrt{2}$是同类二次根式的是( )| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\sqrt{8}$ | D. | $\sqrt{12}$ |
分析 直接利用同类二次根式的定义分别分析得出答案.
解答 解:A、$\sqrt{3}$与3$\sqrt{2}$不是同类二次根式,故此选项错误;
B、$\sqrt{6}$与3$\sqrt{2}$不是同类二次根式,故此选项错误;
C、$\sqrt{8}$=2$\sqrt{2}$与3$\sqrt{2}$是同类二次根式,故此选项正确;
D、$\sqrt{12}$=2$\sqrt{3}$,不是同类二次根式,故此选项错误;
故选:C.
点评 此题主要考查了同类二次根式,正确把握定义是解题关键.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
14.下面的每组图形中,平移左图可以得到右图的一组是( )
| A. |  | B. |  | C. |  | D. |  |
15.若a>b,则下列不等式中成立的是( )
| A. | a+3<b+3 | B. | a-3<b-3 | C. | 3a<3b | D. | -3a<-3b |
16.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{48}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{4a+12}$ |
13.如果线段a,b,c能组成直角三角形,则它们的比可以是( )
| A. | 1:2:4 | B. | 1:3:5 | C. | 6:4:7 | D. | 5:12:13 |
14.某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总数排列名次,在一分钟内踢100个以上(含100个)为优秀.如表是成绩最好的甲、乙两班各5名学生的比赛数据.(单位:个)
经统计发现甲、乙两班总个数相同,方差分别为46.8,103.2(平方个).试从中位数,方差,优秀率三个方面考虑,哪个班为冠军?
| 1号 | 2号 | 3号 | 4号 | 5号 | 总个数 | |
| 甲班 | 89 | 100 | 98 | 110 | 103 | 500 |
| 乙班 | 100 | 89 | 97 | 119 | 95 | 500 |
 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示.
甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示.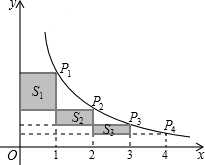 如图,在反比例函数$y=\frac{k}{x}$(x>0)的图象上有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴和y轴的垂线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3,若S1+S2+S3=2.4,则k的值为3.2.
如图,在反比例函数$y=\frac{k}{x}$(x>0)的图象上有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴和y轴的垂线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3,若S1+S2+S3=2.4,则k的值为3.2.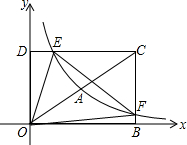 如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0),若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0),若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.