题目内容
如图,正方形ABCD的边 长是4,点P是边CD上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PE,在边AD延长线上取点F,使DF=DP
长是4,点P是边CD上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PE,在边AD延长线上取点F,使DF=DP ,连接EF,CF路。
,连接EF,CF路。
(1)求证:四边形PCFE是平行四边形;
(2)当点P在边CD上运动时,四边形PCFE的面积是否有最大值?若有,请求出面积的最大值及此时CP长;若没有,请说明理由。
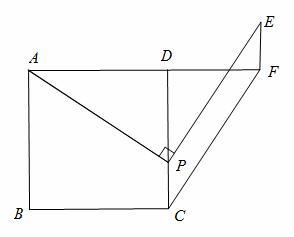
解:(1)∵四边形ABCD是正方形,∴AD=CD,∠ADP=∠CDF=90°。
∵在△ADP和△CDF中,AD=CD,∠ADP=∠CDF,DP=DF,
∴△ADP≌△CDF(SAS)。∴PA=FC,∠PAD=∠FCD。
∵PA=PE, ∴PE=FC。
∴PE=FC。
∵∠PAD+∠APD=90°,∠EPA=90°,∴∠PAD =∠DPE。
∴∠FCD =∠DPE。
=∠DPE。
∴EP∥FC。
∴四边形EPCF是平行四边形。
∴EP∥FC,∴四边形EPCF是平行四边形。
(2) 有。
有。
设CP=x,则DP=4﹣x ,平行四边形PEFC的面积为S,
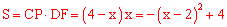 。
。
∵a= ﹣1<0,∴抛物线的开口向下,
﹣1<0,∴抛物线的开口向下,
∴当x=2 时,S最大=4。
∴当CP=2 时,四边形PCFE的面积最大,最大值为4。
【考点】四边形综合题,旋 转问题,正方形的
转问题,正方形的 性质,全等三角形的判定和性质,平行四边形的判定和性质,由实际问题列函数关系式,二次函数的最值。
性质,全等三角形的判定和性质,平行四边形的判定和性质,由实际问题列函数关系式,二次函数的最值。


练习册系列答案
相关题目
 CB=90°,∠ABC=30°,则cosα的值是【 】
CB=90°,∠ABC=30°,则cosα的值是【 】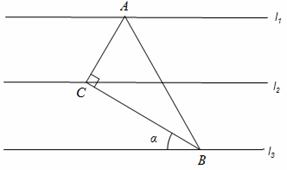
 B.
B. 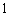 C.
C. 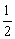 D.
D. 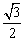
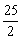 ,DP=8,随着a的大小的变化,点M的位置也在变化.当点M落在矩形ABCD内部时,求a的取值范围。
,DP=8,随着a的大小的变化,点M的位置也在变化.当点M落在矩形ABCD内部时,求a的取值范围。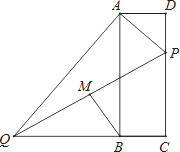
 ,动点P从点B出发,沿B-C-D的路线向点D运动。设△ABP的面积为y (B、P两点重合时,△ABP的面积可以看做0),点P运动的路程为x,则y与x之间函数关系的
,动点P从点B出发,沿B-C-D的路线向点D运动。设△ABP的面积为y (B、P两点重合时,△ABP的面积可以看做0),点P运动的路程为x,则y与x之间函数关系的 图像大致为【 】
图像大致为【 】
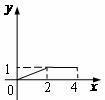
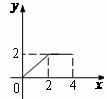 C.
C. 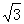 ),C(1,
),C(1, 1个单位的速度向点O运动,动
1个单位的速度向点O运动,动 点Q也同时从点A沿A→B→ C→O的线路以每秒2个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P、
点Q也同时从点A沿A→B→ C→O的线路以每秒2个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P、 Q运动的时间为t(秒)。求△OPQ的面积S与时间t的函数关系式。
Q运动的时间为t(秒)。求△OPQ的面积S与时间t的函数关系式。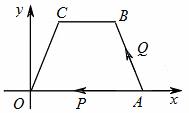
 BCD,其中AB=
BCD,其中AB= 2,AD=1,将矩形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为
2,AD=1,将矩形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为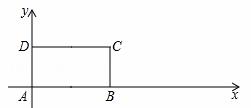
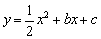
 与
与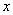
 轴交于A (-4,0) 和B(1,0)两点,与
轴交于A (-4,0) 和B(1,0)两点,与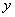
 轴交于C点.
轴交于C点.
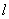
 .
. 点D恰好落在垂线
点D恰好落在垂线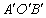
 ,当点O′与点E重合时停止平移.设平移的时间为t秒,△
,当点O′与点E重合时停止平移.设平移的时间为t秒,△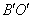
 与线段
与线段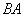
 交于点P,连接
交于点P,连接
 ,
,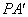
 ,
,
 ,是否存在这样的t,使△
,是否存在这样的t,使△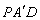
 是等腰三角形?若存在,求出t的值;若不存在,请说明理由.
是等腰三角形?若存在,求出t的值;若不存在,请说明理由.

 度,沿射线AB作匀速运动。当P运动到C点时,P、Q都停止运动
度,沿射线AB作匀速运动。当P运动到C点时,P、Q都停止运动 。设点P运动的时间为ts。
。设点P运动的时间为ts。