题目内容
如图9, 已知抛物线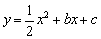
 与
与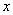
 轴交于A (-4,0) 和B(1,0)两点,与
轴交于A (-4,0) 和B(1,0)两点,与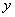
 轴交于C点.
轴交于C点.

(1)求此抛物线的解析式;
(2)设E是线段AB上的动点,作EF//AC交BC于F,连接CE,当△CEF的面积是△BEF面积的2倍时,求E点的坐标;
(3)若P为抛物线上A、C两点间的一个动点,过P作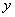
 轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,并求此时P点的坐标.
轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,并求此时P点的坐标.
(1)
 (2)(
(2)(
 ,0) (3)(-2,-3)
,0) (3)(-2,-3)

故E点的坐标为(
 ,0).
,0).

解法二:延长
 交
交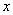
 轴于
轴于
 点,则
点,则
 .要使线段
.要使线段
 最长,则只须△
最长,则只须△
 的面积取大值时即可.
的面积取大值时即可.
设
 点坐标为(
点坐标为(
 ,则有:
,则有: 

=

=

=

=

=
 =-
=-

即
 时,△
时,△
 的面积取大值,此时线段
的面积取大值,此时线段
 最长,则
最长,则
 点坐标为(-2,-3)
点坐标为(-2,-3)


练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
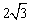 ,经过O,C两点做抛物线
,经过O,C两点做抛物线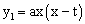 (a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)
(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)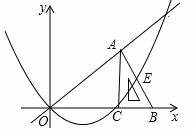
 线
线 的顶点在函数
的顶点在函数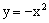 的图象上;
的图象上; 的值。
的值。 长是4,点P是边CD上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PE,在边AD延长线上取点F,使DF=DP
长是4,点P是边CD上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PE,在边AD延长线上取点F,使DF=DP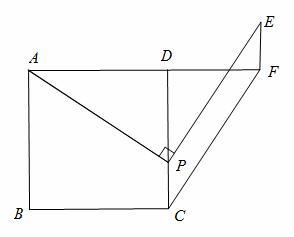



 上的一个动点,抛物线的对称轴与x轴交于点D,经过点P的直线PE与y轴交于点E,是否存在△OPE与△OPD全等?若存在,请求出直线PE的解析式;若不存在,请说明理由。
上的一个动点,抛物线的对称轴与x轴交于点D,经过点P的直线PE与y轴交于点E,是否存在△OPE与△OPD全等?若存在,请求出直线PE的解析式;若不存在,请说明理由。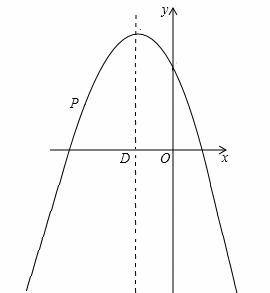



 ,O为坐标原点,抛物线
,O为坐标原点,抛物线 与x轴相交于O、B,顶点为A,连接OA.
与x轴相交于O、B,顶点为A,连接OA. ;
; 其顶点为点C.连接OC和AC,把△AOC沿OA翻折得到四边形ACOC′.试判断其形状,并说明理由;
其顶点为点C.连接OC和AC,把△AOC沿OA翻折得到四边形ACOC′.试判断其形状,并说明理由;