题目内容
6.如图1,直线AB∥CD,P是截线MN上的一点.(1)若∠MNB=45°,∠MDP=20°,求∠MPD;
(2)如图1,当点P在线段MN上运动时,∠CDP与∠ABP的平分线交于Q,问$\frac{∠Q}{∠DPB}$是否为定值,若是定值,请求出;若不是,说明其范围;
(3)如图2,若T是直线MN上且位于M点的上方的一点,如图所示,当点P在射线MT上运动时,∠CDP与∠ABP的平分线交于Q,问$\frac{∠Q}{∠DPB}$的值是否和(2)问中的情况一样呢,请将图形补充完整并说明理由.
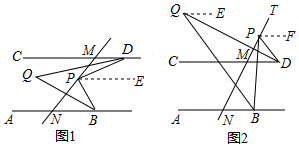
分析 (1)根据AB∥CD、∠MNB=45°可求出∠PMD的度数,在△PMD中利用三角形内角和定理即可求出∠MPD的度数;
(2)过点P作PE∥AB,则PE∥CD,根据平行线的性质可得出∠DPE=∠CDP、∠BPE=∠ABP,进而可得出∠DPB=∠CDP+∠ABP,同理可找出∠Q=∠CDQ+∠ABQ=$\frac{1}{2}$(∠CDP+∠ABP)=$\frac{1}{2}$∠DPB,由此可得出$\frac{∠Q}{∠DPB}$的值为定值$\frac{1}{2}$;
(3)过点P作PE∥AB,过点Q作QE∥AB,则PF∥CD,QE∥CD,根据平行线的性质可得出∠BPF=∠ABP、∠DPF=∠CDP,进而可得出∠DPB=∠ABP-∠CDP,同理可找出∠BQD=∠ABQ-∠CDQ=$\frac{1}{2}$(∠ABP-∠CDP)=$\frac{1}{2}$∠DPB,由此可得出$\frac{∠Q}{∠DPB}$的值为定值$\frac{1}{2}$.
解答 解:(1)∵AB∥CD,∠MNB=45°,
∴∠PMD=180°-45°=135°,
∴∠MPD=180°-∠PMD-∠MDP=180°-135°-20°=25°.
(2)如图1,过点P作PE∥AB,则PE∥CD,
∴∠DPE=∠CDP,∠BPE=∠ABP,
∴∠DPB=∠CDP+∠ABP.
同理:∠Q=∠CDQ+∠ABQ=$\frac{1}{2}$(∠CDP+∠ABP)=$\frac{1}{2}$∠DPB,
∴$\frac{∠Q}{∠DPB}$=$\frac{1}{2}$.
(3)如图2,过点P作PE∥AB,过点Q作QE∥AB,则PF∥CD,QE∥CD,
∴∠BPF=∠ABP,∠DPF=∠CDP,
∴∠DPB=∠BPF-∠DPF=∠ABP-∠CDP.
同理:∠BQD=∠ABQ-∠CDQ=$\frac{1}{2}$(∠ABP-∠CDP)=$\frac{1}{2}$∠DPB,
∴$\frac{∠Q}{∠DPB}$=$\frac{1}{2}$,即(2)的结论仍成立.
点评 本题考查了平行线的性质以及三角形内角和定理,解题的关键是:(1)根据平行线的性质求出∠PMD的度数;(2)利用平行线的性质找出∠DPB=∠CDP+∠ABP、∠Q=$\frac{1}{2}$(∠CDP+∠ABP);(2)利用平行线的性质找出∠DPB=∠ABP-∠CDP、∠BQD=$\frac{1}{2}$(∠ABP-∠CDP).

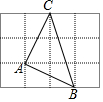 如图,将△ABC放在正方形网格中(图中每个小正方形边长均为1)点A,B,C恰好在网格图中的格点上,那么∠ABC的度数为( )
如图,将△ABC放在正方形网格中(图中每个小正方形边长均为1)点A,B,C恰好在网格图中的格点上,那么∠ABC的度数为( )| A. | 90° | B. | 60° | C. | 30° | D. | 45° |
| A. | -11 | B. | -1 | C. | 1 | D. | 11 |
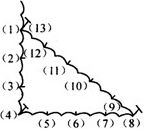 古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )| A. | 直角三角形两个锐角互补 | |
| B. | 三角形内角和等于180° | |
| C. | 如果三角形两条边长的平方和等于第三边长的平方 | |
| D. | 如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形 |
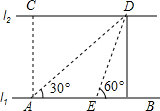 如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.
如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°. 如图,某校把一块三角形的废地ABC改建成一个花园,测得AC=80cm,BC=60cm,AB=100cm.
如图,某校把一块三角形的废地ABC改建成一个花园,测得AC=80cm,BC=60cm,AB=100cm.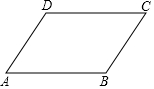 已知ABCD为平行四边形,求证:2(AB2+AD2)=AC2+BD2.
已知ABCD为平行四边形,求证:2(AB2+AD2)=AC2+BD2.