题目内容
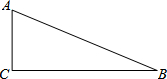 如图,△ABC中,∠C=90°,将△ABC绕点A旋转得到△AB1C1,点C的对应点C1恰好落在AB边上.
如图,△ABC中,∠C=90°,将△ABC绕点A旋转得到△AB1C1,点C的对应点C1恰好落在AB边上.(1)作图:作出△AB1C1(保留作图痕迹,不要求写作法);
(2)已知AC=5,BC=12,求BB1的长.
考点:作图-旋转变换,勾股定理
专题:作图题
分析:(1)以点A为圆心,以AC为半径画弧,与AB相交于点C1,再以点A为圆心,以AB为半径画弧,以C1为圆心,以CB为半径画弧,两弧相交于点B1,然后顺次连接即可;
(2)利用勾股定理列式求出AB,再求出BC1,再利用勾股定理列式计算即可得解.
(2)利用勾股定理列式求出AB,再求出BC1,再利用勾股定理列式计算即可得解.
解答: 解:(1)△AB1C1如图所示;
解:(1)△AB1C1如图所示;
(2)由勾股定理得,AB=
=13,
BC1=13-5=8,B1C1=12,
所以,BB1=
=4
.
 解:(1)△AB1C1如图所示;
解:(1)△AB1C1如图所示;(2)由勾股定理得,AB=
| 52+122 |
BC1=13-5=8,B1C1=12,
所以,BB1=
| 122+82 |
| 13 |
点评:本题考查了利用旋转变换作图,勾股定理的应用,熟练掌握旋转的性质得到对应点的确定方法是解题的关键.

练习册系列答案
相关题目
 如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=6,EF=8,FC=10,则正方形与其外接圆之间形成的阴影部分的面积为( )
如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=6,EF=8,FC=10,则正方形与其外接圆之间形成的阴影部分的面积为( )| A、81π-162 |
| B、80π-160 |
| C、64π-128 |
| D、49π-98 |
 某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象.已知A、B两点相距6米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度.(精确到0.1米,参考数据:
某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象.已知A、B两点相距6米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度.(精确到0.1米,参考数据: 如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数
如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数 为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一组标杆、皮尺,设计了如图所示的测量方案.已知测量同眼睛A标杆顶端F树的顶端E同一直线上,此同学眼睛距地面1.6m标杆长为3.3m且BC=1m,CD=4m,则ED=
为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一组标杆、皮尺,设计了如图所示的测量方案.已知测量同眼睛A标杆顶端F树的顶端E同一直线上,此同学眼睛距地面1.6m标杆长为3.3m且BC=1m,CD=4m,则ED= 如图,在△ABC中,AB=AC,DE∥BC,∠1=65°,则∠2=
如图,在△ABC中,AB=AC,DE∥BC,∠1=65°,则∠2=