题目内容
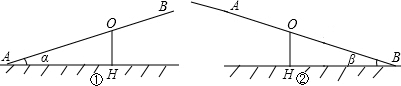
 某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象.已知A、B两点相距6米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度.(精确到0.1米,参考数据:
某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象.已知A、B两点相距6米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度.(精确到0.1米,参考数据:| 2 |
| 3 |
考点:解直角三角形的应用
专题:
分析:过点C作CD⊥AB于点D,设CD=x,在Rt△ACD中表示出AD,在Rt△BCD中表示出BD,再由AB=6米,即可得出关于x的方程,解出即可.
解答: 解:过点C作CD⊥AB于点D,
解:过点C作CD⊥AB于点D,
设CD=x,
在Rt△ACD中,∠CAD=30°,
则AD=
CD=
x,
在Rt△BCD中,∠CBD=45°,
则BD=CD=x,
由题意得
x-x=6,
解得:x═3(
+1)≈8.2.
答:生命所在点C的深度为8.2米.
 解:过点C作CD⊥AB于点D,
解:过点C作CD⊥AB于点D,设CD=x,
在Rt△ACD中,∠CAD=30°,
则AD=
| 3 |
| 3 |
在Rt△BCD中,∠CBD=45°,
则BD=CD=x,
由题意得
| 3 |
解得:x═3(
| 3 |
答:生命所在点C的深度为8.2米.
点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数知识表示出相关线段的长度,注意方程思想的运用.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 已知关于x一元二次方程x2-2(k+1)x+k2-2k-3=0有两个不相等的实数根
已知关于x一元二次方程x2-2(k+1)x+k2-2k-3=0有两个不相等的实数根 在正方形网格中建立如图的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
在正方形网格中建立如图的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题: 在平面直角坐标系xOy中,已知二次函数的图象经过原点及点A(1,2),与x轴相交于另一点B(3,0),将点B向右平移3个单位得点C.
在平面直角坐标系xOy中,已知二次函数的图象经过原点及点A(1,2),与x轴相交于另一点B(3,0),将点B向右平移3个单位得点C. 如图,一只碗,从侧面观察碗身是一条抛物线,而俯视又是一个圆,已知碗深为5cm,碗口宽为10cm,现向碗中加水,使它刚好漂浮四张半径均为2cm的圆形薄纸片,则加入的水深应是多少?
如图,一只碗,从侧面观察碗身是一条抛物线,而俯视又是一个圆,已知碗深为5cm,碗口宽为10cm,现向碗中加水,使它刚好漂浮四张半径均为2cm的圆形薄纸片,则加入的水深应是多少?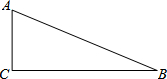 如图,△ABC中,∠C=90°,将△ABC绕点A旋转得到△AB1C1,点C的对应点C1恰好落在AB边上.
如图,△ABC中,∠C=90°,将△ABC绕点A旋转得到△AB1C1,点C的对应点C1恰好落在AB边上. 如图,A、B、C是⊙O上的三个点,且BC=2AB=2,圆心角∠AOC=120°,则⊙O的半径是
如图,A、B、C是⊙O上的三个点,且BC=2AB=2,圆心角∠AOC=120°,则⊙O的半径是