题目内容
 如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数y=
如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数y=| k |
| x |
| 2 |
| 5 |
(1)求反比例函数和一次函数的解析式;
(2)求△OBC的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)解直角三角形求出B的坐标,代入求出反比例函数解析式,求出A的坐标,把A、B的坐标代入一次函数的解析式求出即可;
(2)求出C的坐标,根据三角形面积公式求出即可.
(2)求出C的坐标,根据三角形面积公式求出即可.
解答: 解:(1)过B作BM⊥x轴于M,
解:(1)过B作BM⊥x轴于M,
∵B(n,-2),tan∠BOC=
,
∴BM=2,tan∠BOC=
=
,
∴OM=5,
即B的坐标是(-5,-2),
把B的坐标代入y=
得:k=10,
即反比例函数的解析式是y=
,
把A(2,m)代入得:m=5,
即A的坐标是(2,5),
把A、B的坐标代入y=ax+b得:
,
解得:k=1,b=3,
即一次函数的解析式是y=x+3;
(2)∵把y=0代入y=x+3得:x=-3,
即OC=3,
∴△OBC的面积是
×3×2=3..
 解:(1)过B作BM⊥x轴于M,
解:(1)过B作BM⊥x轴于M,∵B(n,-2),tan∠BOC=
| 2 |
| 5 |
∴BM=2,tan∠BOC=
| 2 |
| OM |
| 2 |
| 5 |
∴OM=5,
即B的坐标是(-5,-2),
把B的坐标代入y=
| k |
| x |
即反比例函数的解析式是y=
| 10 |
| x |
把A(2,m)代入得:m=5,
即A的坐标是(2,5),
把A、B的坐标代入y=ax+b得:
|
解得:k=1,b=3,
即一次函数的解析式是y=x+3;
(2)∵把y=0代入y=x+3得:x=-3,
即OC=3,
∴△OBC的面积是
| 1 |
| 2 |
点评:本题考查了一次函数和反比例函数的交点问题解直角三角形,用待定系数法求一次函数、反比例函数的解析式的应用,主要考查学生的计算能力,题目比较好,难度适中.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
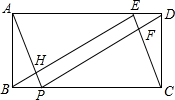 如图:在矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.
如图:在矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.
 在平面直角坐标系xOy中,已知二次函数的图象经过原点及点A(1,2),与x轴相交于另一点B(3,0),将点B向右平移3个单位得点C.
在平面直角坐标系xOy中,已知二次函数的图象经过原点及点A(1,2),与x轴相交于另一点B(3,0),将点B向右平移3个单位得点C.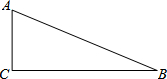 如图,△ABC中,∠C=90°,将△ABC绕点A旋转得到△AB1C1,点C的对应点C1恰好落在AB边上.
如图,△ABC中,∠C=90°,将△ABC绕点A旋转得到△AB1C1,点C的对应点C1恰好落在AB边上.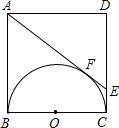 在边长为a的正方形内ABCD中,AE与以BC为直径的半圆相切于点F,交CD于E,求CF、FD的长.
在边长为a的正方形内ABCD中,AE与以BC为直径的半圆相切于点F,交CD于E,求CF、FD的长. 如图,在Rt△ABC中,BC=8,AC=6,∠ACB=90°,分别以A、B为圆心作两个外切的等圆,则图中阴影部分的面积是
如图,在Rt△ABC中,BC=8,AC=6,∠ACB=90°,分别以A、B为圆心作两个外切的等圆,则图中阴影部分的面积是 如图,在斜边为3的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…依次作下去,则第2014个正方形A2014B2014C2014D2014的边长是( )
如图,在斜边为3的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…依次作下去,则第2014个正方形A2014B2014C2014D2014的边长是( )