题目内容
如图，在正方形ABCD内有一折线段，其中AE⊥EF，EF⊥FC，并且AE=6，EF=8，FC=10，则正方形与其外接圆之间形成的阴影部分的面积为（ ）| A、81π-162 |
| B、80π-160 |
| C、64π-128 |
| D、49π-98 |
考点：相似三角形的判定与性质,正方形的性质,正多边形和圆
专题：
分析：首先连接AC，则可证得△AEM∽△CFM，根据相似三角形的对应边成比例，即可求得EM与FM的长，然后由勾股定理求得AM与CM的长，则可求得正方形与圆的面积，进而求出正方形与其外接圆之间形成的阴影部分的面积．
解答：解：连接AC，
∵AE丄EF，EF丄FC，
∴∠E=∠F=90°，
∵∠AME=∠CMF（对顶角相等），
∴△AEM∽△CFM，
∴
=
，
∵AE=6，EF=8，FC=10，
∴
=
=
，
∴EM=3，FM=5，
在Rt△AEM中，AM=
=3
，
在Rt△FCM中，CM=
=5
，
∴AC=8
，
在Rt△ABC中，AB=AC•sin45°=8
×
=4
，
∴S正方形ABCD=AB2=160，
圆的面积为：π•（
）2=80π，
∴正方形与其外接圆之间形成的阴影部分的面积为80π-160．
故选B．
∵AE丄EF，EF丄FC，
∴∠E=∠F=90°，
∵∠AME=∠CMF（对顶角相等），
∴△AEM∽△CFM，
∴
| AF |
| CG |
| EM |
| FM |
∵AE=6，EF=8，FC=10，
∴
| EM |
| FM |
| 6 |
| 10 |
| 3 |
| 5 |
∴EM=3，FM=5，
在Rt△AEM中，AM=
| AE2+EM2 |
| 5 |
在Rt△FCM中，CM=
| CF2+FM2 |
| 5 |
∴AC=8
| 5 |
在Rt△ABC中，AB=AC•sin45°=8
| 5 |
| ||
| 2 |
| 10 |
∴S正方形ABCD=AB2=160，
圆的面积为：π•（
8
| ||
| 2 |
∴正方形与其外接圆之间形成的阴影部分的面积为80π-160．
故选B．
点评：此题考查了相似三角形的判定与性质，正方形与圆的面积的求解方法，以及勾股定理的应用．此题综合性较强，解题时要注意数形结合思想的应用
练习册系列答案
相关题目
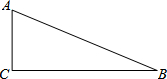如图，△ABC中，∠C=90°，将△ABC绕点A旋转得到△AB1C1，点C的对应点C1恰好落在AB边上．
如图，在斜边为3的等腰直角三角形OAB中，作内接正方形A1B1C1D1；在等腰直角三角形OA1B1中，作内接正方形A2B2C2D2；在等腰直角三角形OA2B2中，作内接正方形A3B3C3D3…依次作下去，则第2014个正方形A2014B2014C2014D2014的边长是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图，已知点A1，A2，…，A2014在函数y=2x2位于第二象限的图象上，点B1，B2，…，
如图，直角梯形OABC中，AB∥OC，点A坐标为（0，6），点C坐标为（3，0），BC=