题目内容
解方程:
+
+…+
=
.
| 1 |
| (x+1)(x+2) |
| 1 |
| (x+2)(x+3) |
| 1 |
| (x+1994)(x+1995) |
| 2x+3987 |
| 3x+5985 |
考点:解分式方程
专题:计算题
分析:分式方程左边利用拆项法变形,抵消合并后求出解即可.
解答:解:分式方程变形得:
-
+
-
+…+
-
=
,
即
=
,
整理得:
=
,
去分母得:2x2+3989x-1995=0,
分解因式得:(x+1995)(2x-1)=0,
解得:x=-1995或x=0.5,
经检验x=-1995与x=0.5是分式方程的解.
| 1 |
| x+1 |
| 1 |
| x+2 |
| 1 |
| x+2 |
| 1 |
| x+3 |
| 1 |
| x+1994 |
| 1 |
| x+1995 |
| 2x+3987 |
| 3x+5985 |
即
| 1994 |
| (x+1)(x+1995) |
| 2x+3987 |
| 3(x+1995) |
整理得:
| 1994 |
| x+1 |
| 2x+3987 |
| 3 |
去分母得:2x2+3989x-1995=0,
分解因式得:(x+1995)(2x-1)=0,
解得:x=-1995或x=0.5,
经检验x=-1995与x=0.5是分式方程的解.
点评:此题考查了解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 已知△ABC的内心为O,∠BOC=110°,则∠BAC=
已知△ABC的内心为O,∠BOC=110°,则∠BAC=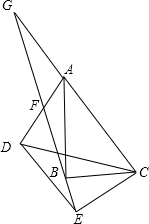 如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,过A作AG∥DE交射线EB于点G,点F恰好是AD中点.
如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,过A作AG∥DE交射线EB于点G,点F恰好是AD中点.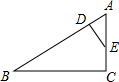 如图所示,在△ABC中,点D、E分别是△ABC的边AB、AC上的点,且AD=3,AE=6,DE=5,BD=15,CE=3,BC=15,根据以上条件,你认为∠B=∠AED吗?
如图所示,在△ABC中,点D、E分别是△ABC的边AB、AC上的点,且AD=3,AE=6,DE=5,BD=15,CE=3,BC=15,根据以上条件,你认为∠B=∠AED吗? 如图,△ABC中,D是AB的黄金分割点(AD<BD),过点D作DE∥BC交AC于E,若BC=3+
如图,△ABC中,D是AB的黄金分割点(AD<BD),过点D作DE∥BC交AC于E,若BC=3+ 如图示角度,CD=100m,求AB的高度?(精确到0.1m,
如图示角度,CD=100m,求AB的高度?(精确到0.1m,