题目内容
已知M、N两点把线段AB分成比例1:4:5的三个部分,C是AN的中点,已知CB=12,求:
(1)AC的长;
(2)MC:CN.
(1)AC的长;
(2)MC:CN.
考点:两点间的距离
专题:
分析:(1)根据线段的比例,可得MN=4AM,NB=5AM,根据线段中点的性质,可得AC与CN,根据线段的和差,可得关于AM的方程,根据解方程,可得AM的长根据AC与AM的关系,可得答案;
(2)根据线段的和差,可得MC、NC的长,根据比的意义,可得答案.
(2)根据线段的和差,可得MC、NC的长,根据比的意义,可得答案.
解答:解:如图 ,
,
(1)由AM:MN:NB=1:4:5,得
MN=4AM,NB=5AM.
由线段的和差,得
AN=AM+MN=4AM+AM=5AM.
由线段中点的性质,得
AC=CN=
AM.
由线段的和差,得
CB=CN+BN=
AM+5AM=12.
解得AM=
.
AC=
AM=
×
=4;
(2)由线段的和差,得
MC=AC-AM=
AM-AM=
AM=
×
=
,
CN=AC=4,
MC:CN=
:4=3:5.
 ,
,(1)由AM:MN:NB=1:4:5,得
MN=4AM,NB=5AM.
由线段的和差,得
AN=AM+MN=4AM+AM=5AM.
由线段中点的性质,得
AC=CN=
| 5 |
| 2 |
由线段的和差,得
CB=CN+BN=
| 5 |
| 2 |
解得AM=
| 8 |
| 5 |
AC=
| 5 |
| 2 |
| 5 |
| 2 |
| 8 |
| 5 |
(2)由线段的和差,得
MC=AC-AM=
| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 8 |
| 5 |
| 12 |
| 5 |
CN=AC=4,
MC:CN=
| 12 |
| 5 |
点评:本题考查了两点间的距离,利用了线段的和差,线段中点的性质,比的意义.

练习册系列答案
相关题目
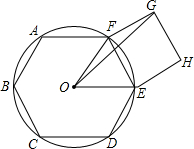 如图,半径为R的圆内,ABCDEF是正六边形,EFGH是正方形.
如图,半径为R的圆内,ABCDEF是正六边形,EFGH是正方形.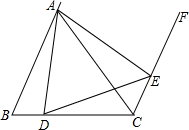 已知等边△ABC,AB∥CF,点D在BC上,E在CF上,∠ADE=60°,问△ADE是等边三角形吗?
已知等边△ABC,AB∥CF,点D在BC上,E在CF上,∠ADE=60°,问△ADE是等边三角形吗? 如图,BD、CE是△ABC的两条高,连接DE.
如图,BD、CE是△ABC的两条高,连接DE.