题目内容
19.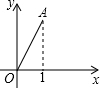 如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )
如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )| A. | (0,2) | B. | (0,-2) | C. | (-1,-$\sqrt{3}$) | D. | ($\sqrt{3}$,1) |
分析 作AD⊥x轴,由点A坐标得出OD=1、AD=$\sqrt{3}$,从而知∠AOD=60°、OA=2,由旋转性质知将点A绕点O顺时针旋转150°得到点B位于y轴负半轴,且OB=OA=2,据此可得答案.
解答 解:如图,作AD⊥x轴于点D,
∵A(1,$\sqrt{3}$),
∴OD=1、AD=$\sqrt{3}$,
则tan∠AOD=$\frac{AD}{OD}$=$\sqrt{3}$,OA=$\sqrt{O{D}^{2}+A{D}^{2}}$=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∴∠AOD=60°,
∴将点A绕点O顺时针旋转150°得到点B位于y轴负半轴,且OB=OA=2,
∴点B的坐标为(0,-2),
故选:B.
点评 本题主要考查坐标与图形的变化-旋转,熟练掌握旋转的定义和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.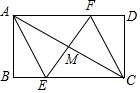 如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )
如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )
 如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )
如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )| A. | AE=CF | B. | AB=AM | C. | AC⊥EF | D. | EF平分∠AEC |
8.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
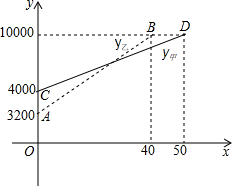 2016年国庆期间,某校准备组织部分教职工到黄山风景区旅游.经市场调研发现.如图,线段CD表示甲旅行社所需总费用y甲(元)与旅游人数x的函数图象,线段AB表示乙旅行社所需总费用y乙(元)与旅游人数x的函数图象,根据图象提供的信息,解答下列问题:
2016年国庆期间,某校准备组织部分教职工到黄山风景区旅游.经市场调研发现.如图,线段CD表示甲旅行社所需总费用y甲(元)与旅游人数x的函数图象,线段AB表示乙旅行社所需总费用y乙(元)与旅游人数x的函数图象,根据图象提供的信息,解答下列问题: 如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.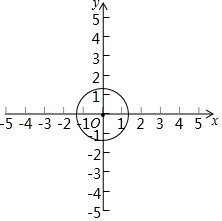 在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),( $\sqrt{2}$,$\sqrt{2}$ ),…,都是梦之点,显然梦之点有无数个.
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),( $\sqrt{2}$,$\sqrt{2}$ ),…,都是梦之点,显然梦之点有无数个.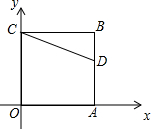 如图,正方形OABC的两边OA,OC分别在x轴上,点D(5,3)在边AB上,以C为中心,把△CDB绕点C顺时针旋转90°,则旋转后点D的对应点D′的坐标是(-2,0).
如图,正方形OABC的两边OA,OC分别在x轴上,点D(5,3)在边AB上,以C为中心,把△CDB绕点C顺时针旋转90°,则旋转后点D的对应点D′的坐标是(-2,0).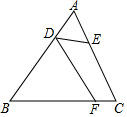 如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:DF∥AC,或∠BFD=∠A,可以使得△FDB与△ADE相似.(只需写出一个)
如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:DF∥AC,或∠BFD=∠A,可以使得△FDB与△ADE相似.(只需写出一个)