题目内容
4.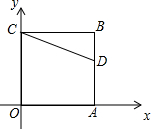 如图,正方形OABC的两边OA,OC分别在x轴上,点D(5,3)在边AB上,以C为中心,把△CDB绕点C顺时针旋转90°,则旋转后点D的对应点D′的坐标是(-2,0).
如图,正方形OABC的两边OA,OC分别在x轴上,点D(5,3)在边AB上,以C为中心,把△CDB绕点C顺时针旋转90°,则旋转后点D的对应点D′的坐标是(-2,0).
分析 作CD′⊥CD交x轴于点D′,证△OCD′≌△BCD即可得知△CDB绕点C顺时针旋转90°点D的对应点即为D′,由OA=OC=OB=5、AD=3知OD′=BD=2,即可得出答案.
解答 解:如图,作CD′⊥CD交x轴于点D′,
∴∠D′CO+∠OCD=90°,
∵四边形OABC是正方形,D(5,3),
∴∠OCD+∠DCB=90°,∠B=∠COD′=90°,OA=OC=OB=5,AD=3,
∴∠OCD′=∠BCD,BD=2,
在△OCD′和△BCD中,
∵$\left\{\begin{array}{l}{∠OCD′=∠BCD}\\{OC=BC}\\{∠COD′=∠B}\end{array}\right.$,
∴△OCD′≌△BCD(ASA),
∴CD=CD′,OD′=BD=2,
∴△CDB绕点C顺时针旋转90°点D的对应点即为D′,其坐标为(-2,0),
故答案为:(-2,0).
点评 本题主要考查图形的旋转及旋转的性质,熟练掌握全等三角形的判定与性质及旋转的性质是解题的关键.

练习册系列答案
相关题目
14.某公园的门票价格如下表所示:
初二(1),(2)两个班共104人计划去游览该公园,其中(1)班人数较少,不足50人;如果两个班都以班为单位分别购票,则一共应付1240.
(1)两个班分别去了多少名学生?
(2)若两班合作团体购票可省多少钱?
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 每人门票价 | 13元 | 11元 | 9元 |
(1)两个班分别去了多少名学生?
(2)若两班合作团体购票可省多少钱?
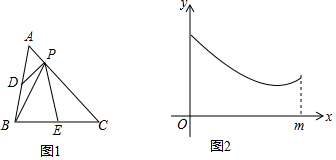
15.如图1,在△ABC中,AB=BC,AC=m,D,E分别是AB,BC边的中点,点P为AC边上的一个动点,连接PD,PB,PE.设AP=x,图1中某条线段长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是( )

| A. | PD | B. | PB | C. | PE | D. | PC |
12.无锡某校准备组织学生及学生家长到上海进行社会实践,为了便于管理,所有人员必须乘坐在同一列火车上:根据报名人数,若都买一等座单程火车票需17010元,若都买二等座单程火车票且花钱最少,则需11220元;已知学生家长与教师的人数之比为2:1,无锡到上海的火车票价格(部分)如表所示:
(1)参加社会实践的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买m张(m小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)w与m之间的函数关系式.
(3)按第(2)小题中的购票方案,请你做一个预算,购买这次单程火车票最少要花多少钱?最多要花多少钱?
| 运行区间 | 公布票价 | 学生票价 | ||
| 上车站 | 下车站 | 一等座 | 二等座 | 三等座 |
| 无锡 | 上海 | 81(元) | 68(元) | 51(元) |
(2)由于各种原因,二等座火车票单程只能买m张(m小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)w与m之间的函数关系式.
(3)按第(2)小题中的购票方案,请你做一个预算,购买这次单程火车票最少要花多少钱?最多要花多少钱?
19.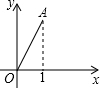 如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )
如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )
 如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )
如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )| A. | (0,2) | B. | (0,-2) | C. | (-1,-$\sqrt{3}$) | D. | ($\sqrt{3}$,1) |
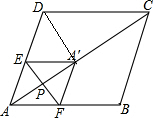 如图,在菱形ABCD中,AB=5,AC=8,P为AC上一动点,过P作EF⊥AC交AD于点E,交AB于点F,将△AEF沿EF折叠,使点A落在对角线AC上的点A′处,当△A′CD为直角三角形时,AP的长为2或$\frac{7}{8}$.
如图,在菱形ABCD中,AB=5,AC=8,P为AC上一动点,过P作EF⊥AC交AD于点E,交AB于点F,将△AEF沿EF折叠,使点A落在对角线AC上的点A′处,当△A′CD为直角三角形时,AP的长为2或$\frac{7}{8}$.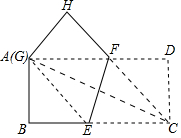 将矩形纸片ABCD(AD>AB)折叠,使点C折叠后的对应点G恰好与A点重合,且折痕分别与边BC、AD相交,设折叠后点C、D的对应点分别为点G、H,折痕分别与边BC、AD相交于点E、F.
将矩形纸片ABCD(AD>AB)折叠,使点C折叠后的对应点G恰好与A点重合,且折痕分别与边BC、AD相交,设折叠后点C、D的对应点分别为点G、H,折痕分别与边BC、AD相交于点E、F.