题目内容
9.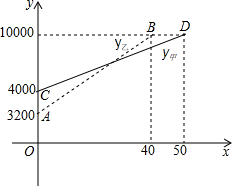 2016年国庆期间,某校准备组织部分教职工到黄山风景区旅游.经市场调研发现.如图,线段CD表示甲旅行社所需总费用y甲(元)与旅游人数x的函数图象,线段AB表示乙旅行社所需总费用y乙(元)与旅游人数x的函数图象,根据图象提供的信息,解答下列问题:
2016年国庆期间,某校准备组织部分教职工到黄山风景区旅游.经市场调研发现.如图,线段CD表示甲旅行社所需总费用y甲(元)与旅游人数x的函数图象,线段AB表示乙旅行社所需总费用y乙(元)与旅游人数x的函数图象,根据图象提供的信息,解答下列问题:(1)分别求出y甲(元)和y乙(元)关于x的函数解析式:
(2)该校如何选择旅行社费用更划算?
(3)该校准备组织10-30(含10和30)名教职工去旅游,如何安排旅游人数和选择哪个旅行社的费用最少?最少费用是多少?
分析 (1)根据待定系数法,可得函数解析式;
(2)根据函数与不等式的关系,可得答案;
(3)根据函数与不等式的关系,可得答案.
解答 解:(1)设甲的解析式为y=kx+b,将(0,4000)(50,10000)代入函数解析式,得
$\left\{\begin{array}{l}{b=4000}\\{50k+b=10000}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=120}\\{b=4000}\end{array}\right.$,
y甲=120x+4000;
设乙的解析式为y=cx+d,将(0,3200)(40,10000)代入函数解析式,得
$\left\{\begin{array}{l}{d=3200}\\{40c+d=10000}\end{array}\right.$,
解得$\left\{\begin{array}{l}{c=170}\\{d=3200}\end{array}\right.$,
y乙=170x+3200;
(2)当y甲=y乙时,120x+4000=170x+3200,
解得x=16,
当0≤x<16时,选择乙合算;
当x=16时,甲与乙都一样;
当16<x<50时,选择甲合算;
(3)当x=10时,选择乙旅行社费用少,费用是1700+3200=20200元;
当x=16时,甲乙旅行社都可以,费用是120×16+4000=5920元;
当x=30时,选择甲旅行社费用少,120×30+4000=7600元.
点评 本题考查了一次函数的应用,利用待定系数法是解(1)的题关键;利用函数与不等式的关系是解(2)(3)的题关键;

练习册系列答案
相关题目
4.某蔬菜基地打算将115吨的蔬菜运往县城销售,现找到一物流公司有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示(假设每辆车均满载,并且每种车型数量足够):
(1)若全部蔬菜都用甲、乙两种车型来运送,需运费7800元,问分别需甲、乙两种车型各几辆?
(2)蔬菜基地计划用甲、乙、丙三种车型共15辆同时参与运送,将全部蔬菜运往县城销售,如何安排装运,可使运费最省?最省运费是多少?
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
(2)蔬菜基地计划用甲、乙、丙三种车型共15辆同时参与运送,将全部蔬菜运往县城销售,如何安排装运,可使运费最省?最省运费是多少?
14.某公园的门票价格如下表所示:
初二(1),(2)两个班共104人计划去游览该公园,其中(1)班人数较少,不足50人;如果两个班都以班为单位分别购票,则一共应付1240.
(1)两个班分别去了多少名学生?
(2)若两班合作团体购票可省多少钱?
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 每人门票价 | 13元 | 11元 | 9元 |
(1)两个班分别去了多少名学生?
(2)若两班合作团体购票可省多少钱?
19.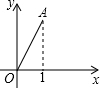 如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )
如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )
 如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )
如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )| A. | (0,2) | B. | (0,-2) | C. | (-1,-$\sqrt{3}$) | D. | ($\sqrt{3}$,1) |
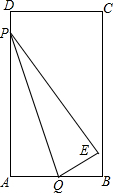 如图,矩形纸ABCD,AB=3,AD=6,动点Q从点A出发以每秒1个单位长的速度沿AB向终点B运动,运动$\frac{2}{3}$秒时,动点P从点D出发以相等的速度沿DA向终点A运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).将△APQ沿PQ翻折,得到△EPQ
如图,矩形纸ABCD,AB=3,AD=6,动点Q从点A出发以每秒1个单位长的速度沿AB向终点B运动,运动$\frac{2}{3}$秒时,动点P从点D出发以相等的速度沿DA向终点A运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).将△APQ沿PQ翻折,得到△EPQ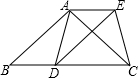 已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.