题目内容
9．
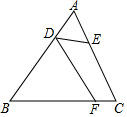如图，在△ABC中，AB≠AC．D、E分别为边AB、AC上的点．AC=3AD，AB=3AE，点F为BC边上一点，添加一个条件：DF∥AC，或∠BFD=∠A，可以使得△FDB与△ADE相似．（只需写出一个）
分析 结论：DF∥AC，或∠BFD=∠A．根据相似三角形的判定方法一一证明即可．
解答 解：DF∥AC，或∠BFD=∠A．
理由：∵∠A=∠A，$\frac{AD}{AC}$=$\frac{AE}{AB}$=$\frac{1}{3}$，
∴△ADE∽△ACB，
∴①当DF∥AC时，△BDF∽△BAC，
∴△BDF∽△EAD．
②当∠BFD=∠A时，∵∠B=∠AED，
∴△FBD∽△AED．
故答案为DF∥AC，或∠BFD=∠A．
点评 本题考查相似三角形的判定和性质．平行线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
练习册系列答案
相关题目
19．
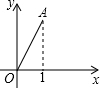如图，在平面直角坐标系中，点A（1，$\sqrt{3}$），若将点A绕点O顺时针旋转150°得到点B，则点B的坐标为（ ）
如图，在平面直角坐标系中，点A（1，$\sqrt{3}$），若将点A绕点O顺时针旋转150°得到点B，则点B的坐标为（ ）| A． | （0，2） | B． | （0，-2） | C． | （-1，-$\sqrt{3}$） | D． | （$\sqrt{3}$，1） |
4．
小莹和小博士下棋，小莹执圆子，小博士执方子．如图，棋盘中心方子的位置用（-1，0）表示，右下角方子的位置用（0，-1）表示．小莹将第4枚圆子放入棋盘后，所有棋子构成一个轴对称图形．她放的位置是（ ）
小莹和小博士下棋，小莹执圆子，小博士执方子．如图，棋盘中心方子的位置用（-1，0）表示，右下角方子的位置用（0，-1）表示．小莹将第4枚圆子放入棋盘后，所有棋子构成一个轴对称图形．她放的位置是（ ）| A． | （-2，1） | B． | （-1，1） | C． | （1，-2） | D． | （-1，-2） |
1．
如图，数轴上两点A，B表示的数互为相反数，则点B表示的数为（ ）
如图，数轴上两点A，B表示的数互为相反数，则点B表示的数为（ ）| A． | -6 | B． | 6 | C． | 0 | D． | 无法确定 |
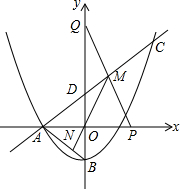如图，抛物线y=$\frac{1}{4}$x2+$\frac{1}{4}$x+c与x轴的负半轴交于点A，与y轴交于点B，连结AB，点C（6，$\frac{15}{2}}$）在抛物线上，直线AC与y轴交于点D．
如图，直线a∥b，∠BAC的顶点A在直线a上，且∠BAC=100°．若∠1=34°，则∠2=46°．