题目内容
14.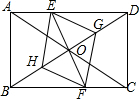 已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.
已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,则四边形EGFH是什么特殊四边形?证明你的结论.
分析 (1)由平行四边形的性质得出AD∥BC,AD=BC,OB=OD,由平行线的性质得出∠FBH=∠EDG,∠OHF=∠OGE,得出∠BHF=∠DGE,求出BF=DE,由AAS即可得出结论;
(2)先证明四边形EGFH是平行四边形,再由等腰三角形的性质得出EF⊥GH,即可得出四边形EGFH是菱形.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OB=OD,
∴∠FBH=∠EDG,
∵AE=CF,
∴BF=DE,
∵EG∥FH,
∴∠OHF=∠OGE,
∴∠BHF=∠DGE,
在△BFH和△DEG中,
$\left\{\begin{array}{l}{∠FBH=∠EDG}&{\;}\\{∠BHF=∠DGE}&{\;}\\{BF=DE}&{\;}\end{array}\right.$,
∴BFH≌△DEG(AAS);
(2)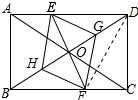 解:四边形EGFH是菱形;理由如下:
解:四边形EGFH是菱形;理由如下:
连接DF,如图所示:
由(1)得:BFH≌△DEG,
∴FH=EG,
又∵EG∥FH,
∴四边形EGFH是平行四边形,
∵BF=DF,OB=OD,
∴EF⊥BD,
∴EF⊥GH,
∴四边形EGFH是菱形.
点评 本题考查了全等三角形的性质和判定,平行线的性质,菱形的判定,等腰三角形的性质,平行四边形的性质和判定等知识;熟练掌握平行四边形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
4. 如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )
如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )
 如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )
如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )| A. | $\frac{12}{25}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
5.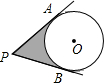 如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
 如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )| A. | 9$\sqrt{3}$-3π | B. | 9$\sqrt{3}$-2π | C. | $\frac{9}{2}\sqrt{3}-3π$ | D. | $\frac{9}{2}\sqrt{3}-2π$ |
2.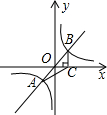 如图,过原点O的直线与双曲线y=$\frac{k}{x}$交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )
如图,过原点O的直线与双曲线y=$\frac{k}{x}$交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )
 如图,过原点O的直线与双曲线y=$\frac{k}{x}$交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )
如图,过原点O的直线与双曲线y=$\frac{k}{x}$交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )| A. | $\frac{5}{3}$ | B. | $\frac{5}{2}$ | C. | 5 | D. | 10 |
19.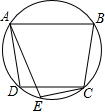 如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )
如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )
 如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )
如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )| A. | 110° | B. | 70° | C. | 80° | D. | 100° |
 如图,C是∠AOB内部一点,D是∠AOB外部一点,在内部求作一点P,使PC=PD,并且使P点到∠AOB两边距离相等(保留作图痕迹).
如图,C是∠AOB内部一点,D是∠AOB外部一点,在内部求作一点P,使PC=PD,并且使P点到∠AOB两边距离相等(保留作图痕迹).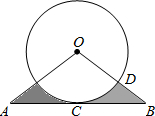 如图,线段AB与⊙O相切于点C,连接OA、OB,OB交⊙O于点D,已知OA=OB=3cm,AB=3$\sqrt{3}$cm,则图中阴影部分的面积为$\frac{9\sqrt{3}}{4}-\frac{3}{4}π$.
如图,线段AB与⊙O相切于点C,连接OA、OB,OB交⊙O于点D,已知OA=OB=3cm,AB=3$\sqrt{3}$cm,则图中阴影部分的面积为$\frac{9\sqrt{3}}{4}-\frac{3}{4}π$. 汽车行驶的路程与时间的关系如图所示,下列说法正确的是( )
汽车行驶的路程与时间的关系如图所示,下列说法正确的是( )