题目内容
2．
如图，在平行四边形ABCD中，∠BAD=60°，AB=6，AC=6$\sqrt{3}$，求?ABCD的面积．
分析 连接BD交AC于点O，过O作OH⊥AB于H，利用已知条件可求出OH的长，再由平行四边形的面积公式计算即可．
解答 
解：如下图，过点C作AD的垂线交AD的延长线于点E，
∵AB=6，∠BAD=60°，
∴DC=6，∠CDE=60°，
又∵CE⊥DE，
∴DE=3，CE=3$\sqrt{3}$，
又∵AE=$\sqrt{{AC}^{2}-C{E}^{2}}$，且AC=$6\sqrt{3}$，
∴AE=9，
∴AD=AE-DE=6，
∴S?ABCD=AD•CE=18$\sqrt{3}$．
点评 本题考查了平行四边形的性质及平行四边形的面积公式的运用，解答本题得关键是求出△ABO的面积．
练习册系列答案
相关题目
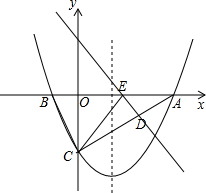已知：如图，对称轴为直线$x=\frac{3}{2}$的抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于点C，连接BC、AC，且OB=$\frac{1}{2}$OA=$\frac{1}{3}$OC．
（1）一家住房的结构如图所示，这家房子的主人打算把卧室以外的部分都铺上地砖，至少需要多少m2的地砖？如果每1m2地砖的价格是a元钱，则购买所需地砖至少需要多少元？
如图，正方形ABCD、DEFH的边长都是5cm，点P从点D出发，先到点A，然后沿箭头所指方向运动（经过点D时不拐弯），则从出发开始连续运动2014cm时，它离点C 最近，此时它距该点1cm．