题目内容
14.抛物线y=x2+bx+3,当实数b变化时,它的顶点都在某条抛物线f上,求f的解析式.分析 根据抛物线y=x2+bx+3的顶点坐标,然后变形即可得到所求抛物线的解析式.
解答 解:∵y=x2+bx+3的顶点坐标是(-$\frac{b}{2}$,$\frac{12-{b}^{2}}{4}$),
设x=-$\frac{b}{2}$,y=$\frac{12-{b}^{2}}{4}$,
∴b=-2x,
∴y=$\frac{12-{b}^{2}}{4}$=$\frac{12-(-2x)^{2}}{4}$=-x2+3,
∴f的解析式为y=-x2+3.
点评 本题考查的是二次函数的性质,熟知二次函数的顶点坐标是解答此题的关键.

练习册系列答案
相关题目
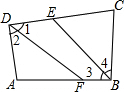 如图,在四边形ABCD中,∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F.
如图,在四边形ABCD中,∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F.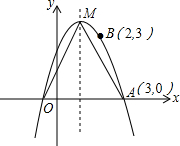 如图,已知抛物线y=-x2+bx+c过点A(3,0)、B(2,3),其顶点为M.
如图,已知抛物线y=-x2+bx+c过点A(3,0)、B(2,3),其顶点为M. 如图,在平行四边形ABCD中,∠BAD=60°,AB=6,AC=6$\sqrt{3}$,求?ABCD的面积.
如图,在平行四边形ABCD中,∠BAD=60°,AB=6,AC=6$\sqrt{3}$,求?ABCD的面积.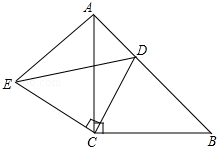 已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.猜想BD2、AD2、CD2之间的关系,并证明.
已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.猜想BD2、AD2、CD2之间的关系,并证明.