题目内容

9．已知：m、n是整数，m+n是奇数，求证：m、n不能全为奇数．

分析 首先假设m，n都为奇数，进而利用有理数的性质得出矛盾，进而得出原命题正确．

解答 证明：设m，n都为奇数
则m=2A+1，n=2B+1．
m+n=2（A+B+1）为偶数，与已知矛盾，
所以mn不能全为奇数．

点评 此题主要考查了反证法，正确从结论的反面出发得出矛盾是解题关键．

练习册系列答案
相关题目
19．某旅行社为吸引市民去某农业观光园区一日游，推出了如下收费标准：如果人数不超过30人，人均旅游费用为100元；如果人数超过30人，每增加10人，人均旅游费用降低10元，但人均旅游费用不会低于65元．
（1）若有20人到该旅行社报名参加，共缴纳旅游费用2000元；
（2）若有40人到该旅行社报名参加，共缴纳旅游费用3600元；
（3）某企业单位集体组织员工去该农业观光园区一日旅游，共支付给旅行社旅游费用4200元，请问该企业单位这次共有多少员工参加旅游？
20．计算：4.282-4.28×4.56+2.282．
17．已知a2+2ab+b2=0，求代数式a（a+4b）-（a-2b）（a+2b）的值．
4．解下列不等式组，并将解集在数轴上表示出来．
$\left\{\begin{array}{l}{x-\frac{x-2}{2}≤\frac{1+4x}{3}}\\{1+3x＞2（2x-1）}\end{array}\right.$．
14．若y=2$\sqrt{x-2}$+$\sqrt{2-x}$+$\frac{1}{3}$，求$\sqrt{x}+\sqrt{y}$的值．
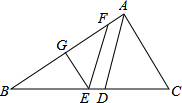1．已知△ABC，∠BAC=80°，AD平分∠BAC，E在BC上，过E分别作EF∥AD交AB于F，作EG∥AC交AB于G，则∠GEF=40°．
18．因式分解：（x+1）2+2x+2．
2．如图，在平行四边形ABCD中，∠BAD=60°，AB=6，AC=6$\sqrt{3}$，求?ABCD的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网