题目内容
直线y=(2-5k)x+3k-2若经过原点,则k= ;若它与x轴交于点(-1,0),则k= .
考点:一次函数图象上点的坐标特征
专题:
分析:先将原点坐标代入直线y=(2-5k)x+3k-2,可求出k的值;再将(-1,0)代入直线y=(2-5k)x+3k-2,可求出k的值.
解答:解:∵直线y=(2-5k)x+3k-2经过原点,
∴3k-2=0,
∴k=
;
将(-1,0)代入直线y=(2-5k)x+3k-2,
得-(2-5k)+3k-2=0,
解得k=
.
故答案为
;
.
∴3k-2=0,
∴k=
| 2 |
| 3 |
将(-1,0)代入直线y=(2-5k)x+3k-2,
得-(2-5k)+3k-2=0,
解得k=
| 1 |
| 2 |
故答案为
| 2 |
| 3 |
| 1 |
| 2 |
点评:本题考查了一次函数图象上点的坐标特征,经过函数的某点一定在函数的图象上.

练习册系列答案
相关题目

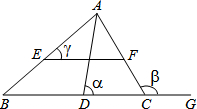 如图,在△ABC中,EF∥BC,∠ACG是△ABC的外角,∠BAC的平分线交BC于点D,记∠ADC=α,∠ACG=β,∠AEF=γ,则:
如图,在△ABC中,EF∥BC,∠ACG是△ABC的外角,∠BAC的平分线交BC于点D,记∠ADC=α,∠ACG=β,∠AEF=γ,则: 如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF,
如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF,