题目内容
 将两个斜边长相等的三角形纸片如图放置,其中∠ACB=∠CED=90°,∠A=45°,∠CDE=30°,∠BCE=15°,则∠ABD的度数为( )
将两个斜边长相等的三角形纸片如图放置,其中∠ACB=∠CED=90°,∠A=45°,∠CDE=30°,∠BCE=15°,则∠ABD的度数为( )| A、40° | B、45° |
| C、50° | D、60° |
考点:三角形内角和定理
专题:
分析:设AB、CD相交于点F,根据直角三角形两锐角互余求出∠BCD=45°,再根据等腰直角三角形的性质可得CF=BF=
AB,CF⊥AB,再求出DF=BF,然后根据等腰三角形两底角相等列式计算即可得解.
| 1 |
| 2 |
解答: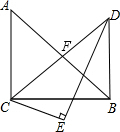 解:如图,设AB、CD相交于点F,
解:如图,设AB、CD相交于点F,
∵∠CED=90°,∠CDE=30°,∠BCE=15°,
∴∠BCD=90°-30°-15°=45°,
∵∠ACB=90°,∠A=45°,
∴△ABC是等腰直角三角形,
∴CF=BF=
AB,CF⊥AB,
∵AB=CD,
∴DF=BF=
AB,
∴∠ABD=
(180°-90°)=45°.
故选B.
 解:如图,设AB、CD相交于点F,
解:如图,设AB、CD相交于点F,∵∠CED=90°,∠CDE=30°,∠BCE=15°,
∴∠BCD=90°-30°-15°=45°,
∵∠ACB=90°,∠A=45°,
∴△ABC是等腰直角三角形,
∴CF=BF=
| 1 |
| 2 |
∵AB=CD,
∴DF=BF=
| 1 |
| 2 |
∴∠ABD=
| 1 |
| 2 |
故选B.
点评:本题考查了三角形的内角和定理,等腰直角三角形的判定与性质,解题的关键在于判断出△ABC是等腰直角三角形并求出BF=DF.

练习册系列答案
相关题目
函数y=-2x2图象是( )
| A、直线 | B、双曲线 |
| C、抛物线 | D、不能确定 |
已知直角三角形ABC的一条直角边AB=4cm,另一条直角边BC=3cm,则以AB为轴旋转一周,所得到的圆锥的侧面积是( )
| A、30πcm2 |
| B、15πcm2 |
| C、12πcm2 |
| D、20πcm2 |
二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
则该函数图象的顶点坐标为( )
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 |
| A、(-1,0) |
| B、(0,-3) |
| C、(1,-4) |
| D、(2,-3) |
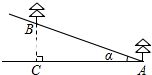 如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.5米范围内,问小明种植的这两棵树是否符合这个要求?
如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.5米范围内,问小明种植的这两棵树是否符合这个要求? 小猫行走在如图所示的图形上,△ABC顶点是正方形网格中,小猫停留在白砖上的概率为
小猫行走在如图所示的图形上,△ABC顶点是正方形网格中,小猫停留在白砖上的概率为 某航空公司规定,乘客所携带行李的重量x(kg)与运费y(元)满足如图所示的函数图象,那么每位乘客最多可免费携带
某航空公司规定,乘客所携带行李的重量x(kg)与运费y(元)满足如图所示的函数图象,那么每位乘客最多可免费携带