题目内容
等腰三角形两边长为3、7,周长为 ;若
+(y+16)2=0,则x+y= .
| x-25 |
考点:等腰三角形的性质,非负数的性质:偶次方,非负数的性质:算术平方根,三角形三边关系
专题:
分析:分3腰长和3是底边长两种情况,根据三角形三边关系讨论求解即可;
利用非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.
利用非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.
解答:解:若3腰长,则三角形的三边分别为3、3、7,
∵3+3=6<7,
∴不能组成三角形,
若3是底边长,则三角形的三边分别为3、7、7,
能组成三角形,
周长=3+7+7=17;
综上所述,三角形的周长为17.
由题意得,x-25=0,y+16=0,
解得x=25,y=-16,
所以,x+y=25+(-16)=9.
故答案为:17;9.
∵3+3=6<7,
∴不能组成三角形,
若3是底边长,则三角形的三边分别为3、7、7,
能组成三角形,
周长=3+7+7=17;
综上所述,三角形的周长为17.
由题意得,x-25=0,y+16=0,
解得x=25,y=-16,
所以,x+y=25+(-16)=9.
故答案为:17;9.
点评:本题考查了等腰三角形的性质,难点在于分情况讨论并利用三角形的三边关系判断是否能组成三角形;非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
相关题目
如果将点A(5,2)向右平移3个单位长度,再向下平移4个单位长度,所得到的点的坐标为( )
| A、(2,6) |
| B、(8,6) |
| C、(2,-2) |
| D、(8,-2) |
 将两个斜边长相等的三角形纸片如图放置,其中∠ACB=∠CED=90°,∠A=45°,∠CDE=30°,∠BCE=15°,则∠ABD的度数为( )
将两个斜边长相等的三角形纸片如图放置,其中∠ACB=∠CED=90°,∠A=45°,∠CDE=30°,∠BCE=15°,则∠ABD的度数为( )| A、40° | B、45° |
| C、50° | D、60° |
命题:①等弧所对的圆周角相等;②三角形的外心到三角形各顶点的距离都相等;③三点确定一个圆;④圆的切线垂直于半径.其中不正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
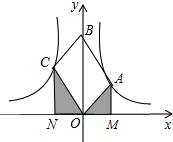 如图,OABC是平行四边形,对角线OB在数轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=
如图,OABC是平行四边形,对角线OB在数轴上,位于第一象限的点A和第二象限的点C分别在双曲线y= 如图,在等边三角形ABC中,BD⊥AC于D,延长BC到E,使CE=CD,AB=6cm.
如图,在等边三角形ABC中,BD⊥AC于D,延长BC到E,使CE=CD,AB=6cm.