题目内容
2.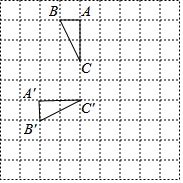 如图,在边长为1的小正方形网格中,将△ABC绕某点旋转到△A'B'C'的位置,则点B运动的最短路径长为$\frac{\sqrt{13}}{2}$π.
如图,在边长为1的小正方形网格中,将△ABC绕某点旋转到△A'B'C'的位置,则点B运动的最短路径长为$\frac{\sqrt{13}}{2}$π.
分析 如图作线段AA′、CC′的垂直平分线相交于点P,点P即为旋转中心,观察图象可知,旋转角为90°(逆时针旋转)时B运动的路径长最短
解答 解: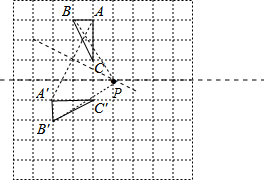 如图作线段AA′、CC′的垂直平分线相交于点P,点P即为旋转中心,
如图作线段AA′、CC′的垂直平分线相交于点P,点P即为旋转中心,
观察图象可知,旋转角为90°(逆时针旋转)时B运动的路径长最短,PB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
∴B运动的最短路径长为=$\frac{90π•\sqrt{13}}{180}$=$\frac{\sqrt{13}}{2}$π,
故答案为$\frac{\sqrt{13}}{2}$π.
点评 本题考查旋转变换、轨迹.弧长公式、勾股定理等知识,解题的关键是确定旋转中心和旋转角的大小,属于中考常考题型.

练习册系列答案
相关题目
14.一个不透明的盒子中装有3个红球,2个白球,这些球除颜色外,没有任何其他区别,从这个盒子中同时随机摸出两个球,所有的可能性如下表:
摸到两个红球的概率为( )
| 红球1 | 红球2 | 红球3 | 白球1 | 白球2 | |
| 红球1 | (红1,红2) | (红1,红3) | (红1,白1) | (红1,白2) | |
| 红球2 | (红2,红3) | (红2,白1) | (红2,白2) | ||
| 红球3 | (红3,白1) | (红3,白2) | |||
| 白球1 | (白1,白2) | ||||
| 白球2 |
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
11.甲、乙、丙、丁四名跳高运动员最近10次训练成绩的平均数与方差如下表所示:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择的是( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数/cm | 180 | 180 | 185 | 185 |
| 方差 | 8.2 | 3.9 | 7.5 | 3.9 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
 如图,在Rt△ABC中,D是斜边AB的中点,连接CD,若∠A=32°,则∠DCB的大小为58°.
如图,在Rt△ABC中,D是斜边AB的中点,连接CD,若∠A=32°,则∠DCB的大小为58°.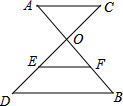 如图,AB、CD相交于点O,OC=4,OD=6,AC∥BD,EF是△ODB的中位线,且EF=4,则AC的长为$\frac{16}{3}$.
如图,AB、CD相交于点O,OC=4,OD=6,AC∥BD,EF是△ODB的中位线,且EF=4,则AC的长为$\frac{16}{3}$. 如图,已知点A的坐标为(5,0),直线y=x+b(b≥0)与y轴交于点B,连接AB,∠α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.
如图,已知点A的坐标为(5,0),直线y=x+b(b≥0)与y轴交于点B,连接AB,∠α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.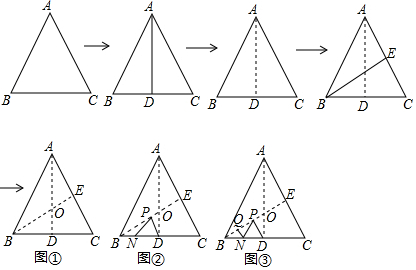
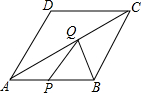 如图,菱形ABCD中,AB=2,∠ADC=120°,P、Q分别是线段AB、AC上的动点,则PQ+BQ的最小值为$\sqrt{3}$.
如图,菱形ABCD中,AB=2,∠ADC=120°,P、Q分别是线段AB、AC上的动点,则PQ+BQ的最小值为$\sqrt{3}$. 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分AB,垂足为点E,请任意写出一组相等的线段BE=EA.
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分AB,垂足为点E,请任意写出一组相等的线段BE=EA.