题目内容
13.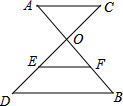 如图,AB、CD相交于点O,OC=4,OD=6,AC∥BD,EF是△ODB的中位线,且EF=4,则AC的长为$\frac{16}{3}$.
如图,AB、CD相交于点O,OC=4,OD=6,AC∥BD,EF是△ODB的中位线,且EF=4,则AC的长为$\frac{16}{3}$.
分析 根据三角形中位线定理求出BD,根据相似三角形的性质列出比例式,计算即可.
解答 解:∵EF是△ODB的中位线,
∴BD=2EF=8,
∵AC∥BD,
∴$\frac{AC}{BD}$=$\frac{OC}{OD}$,即$\frac{AC}{8}$=$\frac{4}{6}$,
解得,AC=$\frac{16}{3}$,
故答案为:$\frac{16}{3}$.
点评 本题考查的是三角形的中位线的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
5. 如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是( )
如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是( )
 如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是( )
如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是( )| A. | 18$\sqrt{3}$-6π | B. | 4$\sqrt{3}$-$\frac{4}{3}$π | C. | 9$\sqrt{3}$-$\frac{9}{2}$π | D. | 2$\sqrt{3}$-$\frac{2}{3}$π |
3.某农科院要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组统计数据:
则该幼树移植成活的概率估计值为0.8(结果精确到0.1).
| 移植总数 | 100 | 400 | 750 | 1500 | 3500 | 7000 | 9000 | 14000 |
| 成活数 | 83 | 314 | 606 | 1197 | 2810 | 5613 | 7194 | 11208 |
| 成活的频率 | 0.83 | 0.785 | 0.808 | 0.798 | 0.803 | 0.802 | 0.799 | 0.801 |
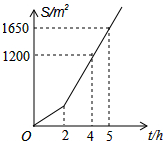 明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是150m2.
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是150m2.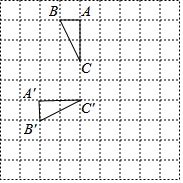 如图,在边长为1的小正方形网格中,将△ABC绕某点旋转到△A'B'C'的位置,则点B运动的最短路径长为$\frac{\sqrt{13}}{2}$π.
如图,在边长为1的小正方形网格中,将△ABC绕某点旋转到△A'B'C'的位置,则点B运动的最短路径长为$\frac{\sqrt{13}}{2}$π.