题目内容
9.图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=$\frac{n(n+1)}{2}$.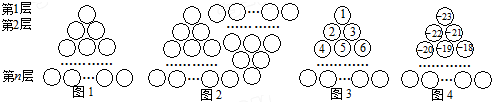
如果图中的圆圈共有11层,请问:自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层中间这个圆圈中的数是61;自上往下,在每个圆圈中按图4的方式填上一串连续的整数
-23,-22,-21,-20,…,则所有圆圈中各数之和为627.
分析 ①第11层中间的数,是第10层最后一个数加上6;
②首先计算第11层圆圈的个数,从而分析出23个负数后,又有多少个正数,最后再相加即可.
解答 解:第10层最后一个数为:10(10+1)÷2=55,所以第11层中间一个数为:55+6=61,
图4中所有圆圈的个数为:1+2+3+…+11=11(11+1)÷2=66个数,其中23个负数,1个0,42个正数,
所以图4中所有圆圈中各数之和=-23-22-21…-1+0+1+2+…+42=(1+2+3+…+42)-(1+2+3+…+23)=42(42+1)÷2-23(23+1)÷2=903-276=627.
故答案为:61;627.
点评 本题是图形类的规律题,要求学生通过观察、分析、归纳发现其中的规律,并应用发现的规律解决问题,注意运用已知给的连续整数和的简便算法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.过以下四边形的四个顶点不能作一个圆的是( )
| A. |  等腰梯形 | B. |  矩形 | ||
| C. |  直角梯形 | D. |  对角是90°的四边形 |
20.抛物线y=2x2-2$\sqrt{2}$x+1与x轴的交点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
17.已知a、b、c是△ABC的三边的长,且满足a2+b2+c2=ab+bc+ac,关于此三角形的形状有下列判断:①是锐角三角形;②是直角三角形;③是钝角三角形;④是等边三角形,其中正确说法的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
18.如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )


| A. | ①③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
19.把所有正偶数从小到大排列,并按如下规律分组:(2),(4,6),(8,10,12),(14,16,18,20),…,现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左往右数).如A2=(1,1),A10=(3,2),A18=(4,3),则A2018可表示为( )
| A. | (45,19) | B. | (45,20) | C. | (44,19) | D. | (44,20) |
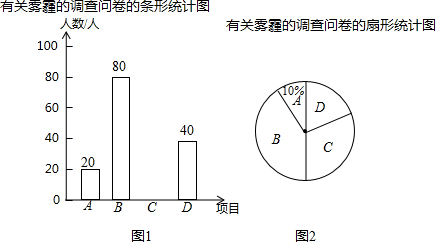 某市对市民看展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:
某市对市民看展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项: