题目内容
11.已知关于x的方程x2+ax+a-3=0.(1)若该方程的一个根为2,求a的值及方程的另一个根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
分析 (1)将x=2代入方程x2+ax+a-3=0得到a的值,再根据根与系数的关系求出另一根;
(2)写出根的判别式,配方后得到完全平方式,进行解答.
解答 解:(1)将x=2代入方程x2+ax+a-3=0得4+2a+a-3=0,解得a=-$\frac{1}{3}$,
方程为x2-$\frac{1}{3}$x-$\frac{10}{3}$=0,即3x2-x-10=0,
解得设x1=-$\frac{5}{3}$,x2=-2.
(2)∵△=a2-4(a-3)
=a2-4a+12
=a2-4a+4+8
=(a-2)2+8>0,
∴不论a取何实数,该方程都有两个不相等的实数根.
点评 本题考查了根的判别式和根与系数的关系,要记牢公式,灵活运用.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
19. 如图,下列条件能判定AD∥BC的是( )
如图,下列条件能判定AD∥BC的是( )
 如图,下列条件能判定AD∥BC的是( )
如图,下列条件能判定AD∥BC的是( )| A. | ∠C=∠CBE | B. | ∠C+∠ABC=180° | C. | ∠FDC=∠C | D. | ∠FDC=∠A |
6.若代数式$\frac{1}{\sqrt{x-1}}$在实数范围内有意义,则x的取值范围是( )
| A. | x>1 | B. | x≥1 | C. | x≠1 | D. | x>0且x≠1 |
20.某不等式的解集x≤-1在数轴上的表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
1.已知,不等式组$\left\{\begin{array}{l}{x>a}\\{-x+5>0}\end{array}\right.$只有3个整数解,则a的取值范围是( )
| A. | 1<x<2 | B. | 1≤x<2 | C. | 1<x≤2 | D. | 1≤x≤2 |
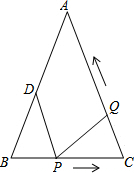 如图,已知△ABC中,AB=AC=10cm,BC=8cm,D为AB的中点,点P在线段BC上由B点出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为ts.
如图,已知△ABC中,AB=AC=10cm,BC=8cm,D为AB的中点,点P在线段BC上由B点出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为ts.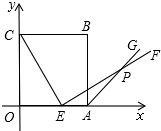 如图,边长为5的正方形OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.
如图,边长为5的正方形OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.