题目内容
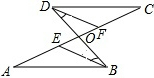 如图,已知:∠A=∠C,∠CDF=∠ABE,求证:∠FDB=∠EBD.
如图,已知:∠A=∠C,∠CDF=∠ABE,求证:∠FDB=∠EBD.考点:平行线的判定与性质
专题:证明题
分析:根据平行线的判定得出DC∥AB,根据平行线的性质得出∠CDO=∠ABO,即可得出答案.
解答:证明:∵∠A=∠C,
∴DC∥AB,
∴∠CDO=∠ABO,
∵∠CDF=∠ABE,
∴∠CDO-∠CDF=∠ABO-∠ABE,
∴∠FDB=∠EBD.
∴DC∥AB,
∴∠CDO=∠ABO,
∵∠CDF=∠ABE,
∴∠CDO-∠CDF=∠ABO-∠ABE,
∴∠FDB=∠EBD.
点评:本题考查了平行线的性质和判定的应用,解此题的关键是求出∠CDO=∠ABO,注意:①内错角相等,两直线平行线,反之亦然.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
点P是线段AB的黄金分割点(PA>PB),则下列结论正确的有( )
①PA2=PB•AB;②
=
;③
=
.
①PA2=PB•AB;②
| PB |
| PA |
| PA |
| PB |
| PB |
| PA |
| ||
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
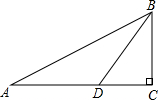 如图,在直角△ABC中,∠C=90°,点D在线段AC上,且∠A=30°,∠BDC=60°,AD=2,则BC=
如图,在直角△ABC中,∠C=90°,点D在线段AC上,且∠A=30°,∠BDC=60°,AD=2,则BC=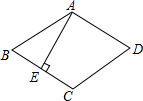 如图,在菱形ABCD中,∠C=120°,AE⊥BC于点E,求证:BE=CE.
如图,在菱形ABCD中,∠C=120°,AE⊥BC于点E,求证:BE=CE.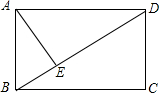 如图,在矩形ABCD中,AE⊥BD,垂足为E,BE=2,ED=6,求矩形ABCD的周长.
如图,在矩形ABCD中,AE⊥BD,垂足为E,BE=2,ED=6,求矩形ABCD的周长.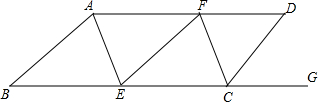 如图,AD∥BC,∠BAD=∠BCD,AE平分∠BAD,CF平分∠BCD.
如图,AD∥BC,∠BAD=∠BCD,AE平分∠BAD,CF平分∠BCD. 如图,已知∠1=∠2,∠A=∠D,求证:∠C=∠F.
如图,已知∠1=∠2,∠A=∠D,求证:∠C=∠F.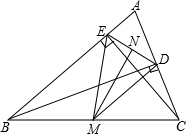 如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,点M、N分别是BC、DE的中点,连接ME、MD.
如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,点M、N分别是BC、DE的中点,连接ME、MD. 如图,在四边形ABCD中,∠A=∠C=∠90°,DE、BF分别是∠ADC、∠ABC的平分线,求证:DE∥BF.
如图,在四边形ABCD中,∠A=∠C=∠90°,DE、BF分别是∠ADC、∠ABC的平分线,求证:DE∥BF.