题目内容
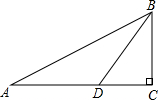 如图,在直角△ABC中,∠C=90°,点D在线段AC上,且∠A=30°,∠BDC=60°,AD=2,则BC=
如图,在直角△ABC中,∠C=90°,点D在线段AC上,且∠A=30°,∠BDC=60°,AD=2,则BC=考点:解直角三角形
专题:计算题
分析:先利用三角形外角性质计算出∠ABD=30°,则∠A=∠ABD,所以BD=AD=2,然后在Rt△BDC中利用∠BDC的正弦可计算出BC的长.
解答:解:∵∠BDC=∠A+∠ABD,
而∠A=30°,∠BDC=60°,
∴∠ABD=30°,
∴∠A=∠ABD,
∴BD=AD=2,
在Rt△BDC中,∵sin∠BDC=
,
∴BC=2sin60°=2×
=
.
故答案为
.
而∠A=30°,∠BDC=60°,
∴∠ABD=30°,
∴∠A=∠ABD,
∴BD=AD=2,
在Rt△BDC中,∵sin∠BDC=
| BC |
| BD |
∴BC=2sin60°=2×
| ||
| 2 |
| 3 |
故答案为
| 3 |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
顺次连结对角线相等的四边形的四边中点所得图形是( )
| A、正方形 | B、矩形 |
| C、菱形 | D、以上都不对 |
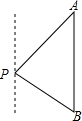 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔60海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔60海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )A、30
| ||
B、30
| ||
| C、60海里 | ||
D、30
|
下列说法中正确的是( )
| A、0没有倒数 |
| B、0没有相反数 |
| C、0没有绝对值 |
| D、平方为0的数不存在 |
 计算阴影部分面积.
计算阴影部分面积. 如图,AB是半圆的直径,AC为弦,OD⊥AB,交AC于点D,垂足为O,⊙O的半径为4,OD=3,求CD的长.
如图,AB是半圆的直径,AC为弦,OD⊥AB,交AC于点D,垂足为O,⊙O的半径为4,OD=3,求CD的长.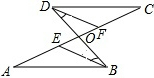 如图,已知:∠A=∠C,∠CDF=∠ABE,求证:∠FDB=∠EBD.
如图,已知:∠A=∠C,∠CDF=∠ABE,求证:∠FDB=∠EBD.