题目内容
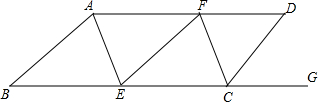 如图,AD∥BC,∠BAD=∠BCD,AE平分∠BAD,CF平分∠BCD.
如图,AD∥BC,∠BAD=∠BCD,AE平分∠BAD,CF平分∠BCD.(1)求证:AE∥CF;
(2)若∠DCG:∠DCF=2:3,求∠AEB的度数.
考点:平行线的判定与性质
专题:
分析:(1)先根据AD∥BC得出∠FAE=∠AEB,再由∠BAD=∠BCD,AE平分∠BAD,CF平分∠BCD可得出∠ECF=∠AEB,故可得出结论;
(2)先根据CF平分∠BCD得出∠ECF=∠DCF,再由∠DCG:∠DCF=2:3可设∠DCG=2x,∠ECF=∠DCE=3x,根据平角的定义求出x的值,再根据(1)中∠ECF=∠AEB即可得出结论.
(2)先根据CF平分∠BCD得出∠ECF=∠DCF,再由∠DCG:∠DCF=2:3可设∠DCG=2x,∠ECF=∠DCE=3x,根据平角的定义求出x的值,再根据(1)中∠ECF=∠AEB即可得出结论.
解答:(1)证明:∵AD∥BC,
∴∠FAE=∠AEB.
∵AE平分∠BAD,CF平分∠BCD,
∴∠FAE=
∠BAD,∠ECF=
∠BCD,
∵∠BAD=∠BCD,
∴∠ECF=∠AEB,
∴AE∥CF;
(2)∵CF平分∠BCD,
∴∠ECF=∠DCF.
∵∠DCG:∠DCF=2:3,
∴设∠DCG=2x,∠ECF=∠DCE=3x,
∴3x+3x+2x=180°,解得x=22.5°,
∴∠ECF=3×22.5°=67.5°.
∵由(1)知∠ECF=∠AEB,
∴∠AEB=67.5°.
∴∠FAE=∠AEB.
∵AE平分∠BAD,CF平分∠BCD,
∴∠FAE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BAD=∠BCD,
∴∠ECF=∠AEB,
∴AE∥CF;
(2)∵CF平分∠BCD,
∴∠ECF=∠DCF.
∵∠DCG:∠DCF=2:3,
∴设∠DCG=2x,∠ECF=∠DCE=3x,
∴3x+3x+2x=180°,解得x=22.5°,
∴∠ECF=3×22.5°=67.5°.
∵由(1)知∠ECF=∠AEB,
∴∠AEB=67.5°.
点评:本题考查的是平行线的判定与性质,用到的知识点为:同位角相等,两直线平行.

练习册系列答案
相关题目
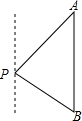 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔60海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔60海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )A、30
| ||
B、30
| ||
| C、60海里 | ||
D、30
|
 如图,在3×2的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的涂法有( )
如图,在3×2的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的涂法有( )| A、1种 | B、2种 | C、3种 | D、4种 |
 如图,在△ABC中,BC=15,AB=12,CP=5,过点P作直线PN与AC交于点N,使截得的三角形与△ABC相似,求PN的长.
如图,在△ABC中,BC=15,AB=12,CP=5,过点P作直线PN与AC交于点N,使截得的三角形与△ABC相似,求PN的长.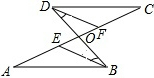 如图,已知:∠A=∠C,∠CDF=∠ABE,求证:∠FDB=∠EBD.
如图,已知:∠A=∠C,∠CDF=∠ABE,求证:∠FDB=∠EBD.