题目内容
5.根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:(1)若a-b>0,则a>b;
(2)若a-b=0,则a=b;
(3)若a-b<0,则a<b.
这种比较大小的方法称为“求差法比较大小”.
请运动这种方法尝试解决下面的问题:
比较4+3a2-2b+b2与3a2-2b+1的大小.
分析 (1)等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变,不等式的两边同时加上b即可;
(2)等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变,等式的两边同时加上b即可;
(3)等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变,不等式的两边同时加上b即可;
(4)求出4+3a2-2b+b2与3a2-2b+1的差的正负,即可比较4+3a2-2b+b2与3a2-2b+1的大小.
解答 解:(1)因为a-b>0,
所以a-b+b>0+b,
即a>b;
(2)因为a-b=0,
所以a-b+b=0+b,
即a=b;
(3)因为a-b<0,
所以a-b+b<0+b,
即a<b.
(4)(4+3a2-2b+b2)-(3a2-2b+1)
=4+3a2-2b+b2-3a2+2b-1
=b2+3
因为b2+3>0,
所以4+3a2-2b+b2>3a2-2b+1.
故答案为:>、=、<.
点评 (1)此题主要考查了不等式的基本性质:(1)不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变;(2)不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;(3)等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变.
(2)此题还考查了“求差法比较大小”方法的应用,要熟练掌握.

练习册系列答案
相关题目
15.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
| A. | AB=CD | B. | AC=BD | C. | AB=BC | D. | AD=BC |
 已知:如图,BD平分∠ABC,BE分∠ABC为2:5两部分,∠DBE=24°,求∠ABE的度数.
已知:如图,BD平分∠ABC,BE分∠ABC为2:5两部分,∠DBE=24°,求∠ABE的度数.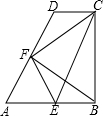 如图,在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连接EF、EC、BF、CF.则①四边形AECD为平行四边形;②△AEF为等边三角形;③△FDC与△BEF为全等的等腰三角形;④△AFB≌△EFC,其中正确的结论有①②③④(写出正确的序号即可)
如图,在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连接EF、EC、BF、CF.则①四边形AECD为平行四边形;②△AEF为等边三角形;③△FDC与△BEF为全等的等腰三角形;④△AFB≌△EFC,其中正确的结论有①②③④(写出正确的序号即可)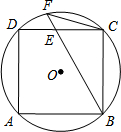 如图,⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,则弦FC的长为$\frac{\sqrt{10}}{5}$.
如图,⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,则弦FC的长为$\frac{\sqrt{10}}{5}$.