题目内容
13.已知点A为反比例函数y=$\frac{6}{x}$(x>0)的图象上的任一点,过点A的直线与双曲线(第一象限图象)只有一个交点,则该直线与坐标轴围成的三角形面积是( )| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
分析 设A点横坐标为a,可得A点坐标(a,$\frac{6}{a}$),再设过点A的直线l的解析式为y=bx+c,根据条件“过点A的直线与双曲线(第一象限图象)只有一个交点”,将A点坐标代入直线l的解析式,得到方程bx+$\frac{6}{a}$-ab=$\frac{6}{x}$,即bx2+($\frac{6}{a}$-ab)x-6=0有两个相等的实根,那么b=-$\frac{6}{{a}^{2}}$,c=$\frac{12}{a}$,即直线l的解析式为y=-$\frac{6}{{a}^{2}}$x+$\frac{12}{a}$.再求出直线l与两坐标轴的交点,进而求解即可.
解答 解:设点A的坐标为(a,$\frac{6}{a}$),其中a>0.过点A的直线l的解析式为y=bx+c,
则ab+c=$\frac{6}{a}$,即c=$\frac{6}{a}$-ab,那么y=bx+$\frac{6}{a}$-ab.
∵直线y=bx+$\frac{6}{a}$-ab与双曲线y=$\frac{6}{x}$只有一个交点,
∴方程bx+$\frac{6}{a}$-ab=$\frac{6}{x}$,即bx2+($\frac{6}{a}$-ab)x-6=0有两个相等的实根,
∴($\frac{6}{a}$-ab)2+24b=($\frac{6}{a}$+ab)2=0.
∴$\frac{6}{a}$=-ab.
∴b=-$\frac{6}{{a}^{2}}$,c=$\frac{12}{a}$,
∴直线l的解析式为y=-$\frac{6}{{a}^{2}}$x+$\frac{12}{a}$.
∴当x=0时,y=$\frac{12}{a}$;当y=0时,x=2a;
∴该直线与坐标轴围成的三角形面积=$\frac{1}{2}$×$\frac{12}{a}$×2a=12.
故选B.
点评 本题考查了反比例函数与一次函数的交点问题,反比例函数图象上点的坐标特征,待定系数法求一次函数的解析式,根的判别式,一次函数与坐标轴的交点坐标,三角形的面积,有一定难度.设A点横坐标为a,用含a的式子表示过点A的直线l的解析式是解题的关键.

 如图所示,数轴的正半轴上有A、B、C三点,表示1和$\sqrt{2}$的对应点分别为A、B,点B到点A的距离与点C到点O的距离相等,设点C所表示的数为x.
如图所示,数轴的正半轴上有A、B、C三点,表示1和$\sqrt{2}$的对应点分别为A、B,点B到点A的距离与点C到点O的距离相等,设点C所表示的数为x.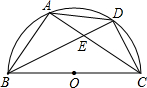 如图,BC是半圆O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E,CE=$\sqrt{5}$,CD=2.
如图,BC是半圆O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E,CE=$\sqrt{5}$,CD=2.