题目内容
19.如果a=2+$\sqrt{3}$,b=$\frac{1}{2-\sqrt{3}}$,那么( )| A. | a>b | B. | a<b | C. | a=b | D. | a=$\frac{1}{b}$ |
分析 根据分母有理化先化简b,再比较a与b的大小即可.
解答 解:b=$\frac{1}{2-\sqrt{3}}$=$\frac{2+\sqrt{3}}{(2-\sqrt{3})(2+\sqrt{3})}$=2+$\sqrt{3}$,
∵a=2+$\sqrt{3}$,
∴a=b,
故选C.
点评 本题考查了分母有理化,二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
9.若(y+3)(y-2)=y2+my+n,则m、n的值分别为( )
| A. | 5;6 | B. | 5;-6 | C. | 1;6 | D. | 1;-6 |
4.顺次连结矩形四边的中点所得的四边形是( )
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 以上都不对 |
8.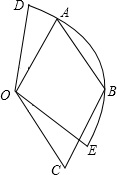 如图,四边形OCBC是菱形,点A、B在以点O为圆心的圆弧DE上,若AO=3,∠COE=∠DOA,则扇形ODE的面积为( )
如图,四边形OCBC是菱形,点A、B在以点O为圆心的圆弧DE上,若AO=3,∠COE=∠DOA,则扇形ODE的面积为( )
 如图,四边形OCBC是菱形,点A、B在以点O为圆心的圆弧DE上,若AO=3,∠COE=∠DOA,则扇形ODE的面积为( )
如图,四边形OCBC是菱形,点A、B在以点O为圆心的圆弧DE上,若AO=3,∠COE=∠DOA,则扇形ODE的面积为( )| A. | $\frac{2}{3}$π | B. | 2π | C. | $\frac{5}{2}$π | D. | 3π |
 小明从家里出发到超市买东西,再回到家,他离家的距离y(千米)与时间t(分钟)的关系如图所示.请你根据图象回答下列问题:
小明从家里出发到超市买东西,再回到家,他离家的距离y(千米)与时间t(分钟)的关系如图所示.请你根据图象回答下列问题: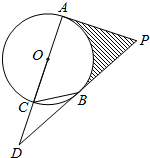 如图,已知PA、PB是⊙O的切线,A、B为切点.直径AC的延长线与PB的延长线交于点D.
如图,已知PA、PB是⊙O的切线,A、B为切点.直径AC的延长线与PB的延长线交于点D.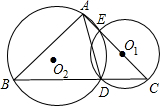 如图,⊙O1和⊙O2相交于点E,D,EC是⊙O1的直径,CE的延长线交⊙O2于点A,CD的延长线交⊙O2于点B.已知CE=4,BD=$\sqrt{13}$,∠C=60°.求:
如图,⊙O1和⊙O2相交于点E,D,EC是⊙O1的直径,CE的延长线交⊙O2于点A,CD的延长线交⊙O2于点B.已知CE=4,BD=$\sqrt{13}$,∠C=60°.求: