题目内容
11.甲做160个零件所用的时间与乙做120个零件所用的时间相同,已知每小时甲、乙两人共做了35个零件,那么每小时甲、乙各做了多少个零件?分析 首先设甲每小时做x个机器零件,则乙每小时做(35-x)个机器零件,根据关键语句“甲做160个零件所用的时间与乙做120个零件所用的时间相同”列出方程,再解即可.
解答 解:设甲每小时做x个机器零件,则乙每小时做(35-x)个机器零件,由题意得:
$\frac{160}{x}$=$\frac{120}{35-x}$,
解得:x=20,
经检验:x=20是原分式方程的解,
则35-20=15(个).
答:甲每小时做20个机器零件,则乙每小时做15个机器零件.
点评 此题主要分式方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程,注意分式方程不要忘记检验.

练习册系列答案
相关题目
1.已知一组数据:12,5,9,5,14,下列说法不正确的是( )
| A. | 方差是8.02 | B. | 中位数是9 | C. | 众数是5 | D. | 极差是9 |
2.设m是方程x2+5x=0的较小的根,n是方程x2+3x+2=0的较小的根,则关于x的一元二次方程x2+mx-n=0的叙述正确的是( )
| A. | 无实根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 不确定 |
19.如果a=2+$\sqrt{3}$,b=$\frac{1}{2-\sqrt{3}}$,那么( )
| A. | a>b | B. | a<b | C. | a=b | D. | a=$\frac{1}{b}$ |
6.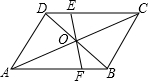 如图,?ABCD中,EF过对角线的交点O分别与CD、AB交于点E、F,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )
如图,?ABCD中,EF过对角线的交点O分别与CD、AB交于点E、F,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )
 如图,?ABCD中,EF过对角线的交点O分别与CD、AB交于点E、F,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )
如图,?ABCD中,EF过对角线的交点O分别与CD、AB交于点E、F,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )| A. | 8.3 | B. | 9.6 | C. | 12.6 | D. | 13.6 |
3.如果a=(-2015)0、b=(-$\frac{1}{10}$)-1、c=(-$\frac{5}{3}$)2,那么a、b、c的大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | c>a>b |
 如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=45cm,当它的一端B着地时,另一端A离地面的高度AC为90cm.
如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=45cm,当它的一端B着地时,另一端A离地面的高度AC为90cm.