题目内容
10. 小明从家里出发到超市买东西,再回到家,他离家的距离y(千米)与时间t(分钟)的关系如图所示.请你根据图象回答下列问题:
小明从家里出发到超市买东西,再回到家,他离家的距离y(千米)与时间t(分钟)的关系如图所示.请你根据图象回答下列问题:(1)小明家离超市的距离是3千米;
(2)小明在超市买东西的时间为1小时;
(3)小明去超市时的速度是15千米/小时.
分析 (1)根据函数图象的纵坐标,可得答案;
(2)根据函数图象的横坐标,可得答案;
(3)根据函数图象的纵坐标,可得距离,根据函数图象的横坐标,可得时间,根据路程与时间的关系,可得答案.
解答 解:(1)由纵坐标看出,小明家离超市的距离是3千米;
(2)由横坐标看出到达超市是12,离开超市是72,在超市的时间为72-12=60分钟=1(小时);
(3)由纵坐标看出,小明家离超市的距离是3千米,由横坐标看出到达超市是12分钟=$\frac{1}{5}$小时,
小明去超市时的速度是3÷$\frac{1}{5}$=15千米/小时;
故答案为:3,1,15.
点评 本题考查了函数图象,观察函数图象获得有效信息是解题关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
20.关于点到直线的距离的四种说法正确的是( )
| A. | 连接直线外的点和直线上的点的线段叫做点到直线的距离 | |
| B. | 连接直线外的点和直线上的点的线段的长度叫做点到直线的距离 | |
| C. | 直线外一点到这条直线的垂线段叫做这点到直线的距离 | |
| D. | 直线外一点到这条直线的垂线段的长度叫做这点到直线的距离 |
1.已知一组数据:12,5,9,5,14,下列说法不正确的是( )
| A. | 方差是8.02 | B. | 中位数是9 | C. | 众数是5 | D. | 极差是9 |
18.下列说法中,不正确的是( )
| A. | 同位角相等,两直线平行 | |
| B. | 两直线被第三条直线所截,内错角相等 | |
| C. | 两直线平行,内错角相等 | |
| D. | 同旁内角互补,两直线平行 |
5.在圆的面积公式S=πr2中,是常量的是( )
| A. | S | B. | π | C. | r | D. | S和r |
2.设m是方程x2+5x=0的较小的根,n是方程x2+3x+2=0的较小的根,则关于x的一元二次方程x2+mx-n=0的叙述正确的是( )
| A. | 无实根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 不确定 |
19.如果a=2+$\sqrt{3}$,b=$\frac{1}{2-\sqrt{3}}$,那么( )
| A. | a>b | B. | a<b | C. | a=b | D. | a=$\frac{1}{b}$ |
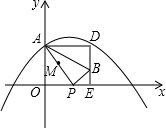 如图,在平面直角坐标系xOy中,抛物线y=ax2+$\frac{5}{6}$x+c过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过点B作x轴的垂线、过点A作y轴的垂线,两直线相交于点D.
如图,在平面直角坐标系xOy中,抛物线y=ax2+$\frac{5}{6}$x+c过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过点B作x轴的垂线、过点A作y轴的垂线,两直线相交于点D.