题目内容
8.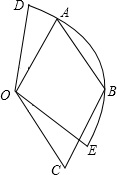 如图,四边形OCBC是菱形,点A、B在以点O为圆心的圆弧DE上,若AO=3,∠COE=∠DOA,则扇形ODE的面积为( )
如图,四边形OCBC是菱形,点A、B在以点O为圆心的圆弧DE上,若AO=3,∠COE=∠DOA,则扇形ODE的面积为( )| A. | $\frac{2}{3}$π | B. | 2π | C. | $\frac{5}{2}$π | D. | 3π |
分析 连接OB.根据等边三角形的性质可以求得∠AOC=120°,再结合∠COE=∠DOA,即可求得扇形所在的圆心角的度数,从而根据扇形的面积公式进行求解.
解答  解:连接OB.
解:连接OB.
∵OA=OB=OC=AB=BC,
∴∠AOB=∠COB=60°,
∴∠AOB+∠BOC=120°.
又∵∠COE=∠DOA,
∴∠DOE=120°.
∴扇形ODE的面积为$\frac{120π×9}{360}$=3π.
故选D.
点评 此题综合运用了菱形的性质、等边三角形的性质和扇形的面积公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.下列说法中,不正确的是( )
| A. | 同位角相等,两直线平行 | |
| B. | 两直线被第三条直线所截,内错角相等 | |
| C. | 两直线平行,内错角相等 | |
| D. | 同旁内角互补,两直线平行 |
19.如果a=2+$\sqrt{3}$,b=$\frac{1}{2-\sqrt{3}}$,那么( )
| A. | a>b | B. | a<b | C. | a=b | D. | a=$\frac{1}{b}$ |
3.如果a=(-2015)0、b=(-$\frac{1}{10}$)-1、c=(-$\frac{5}{3}$)2,那么a、b、c的大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | c>a>b |
18.2014年12月16日,记者从郑州航空港经济综合实验区获悉,2014年前11个月实验区手机产量首次突破1亿部大关,其中富士康手机产量达1.0144亿部,其他手机企业产量超过400万部,预计今年该区手机产量将达到1.4亿部,约占全球手机供货量的八分之一,1.4亿部用科学记数法表示为( )
| A. | 1.4×104部 | B. | 1.4×108亿部 | C. | 1.4×108部 | D. | 1.4×109部 |