题目内容
7.若x=-2是关于x的一元二次方程x2-$\frac{5}{2}$ax+a2=0的一个根,则a的值为-1或-4.分析 把x=-2代入已知方程,列出关于a的新方程,通过解新方程可以求得a的值.
解答 解:∵x=-2是关于x的一元二次方程x2-$\frac{5}{2}$ax+a2=0的一个根,
∴(-2)2-$\frac{5}{2}$a×(-2)+a2=0,即a2+5a+4=0,
整理,得(a+1)(a+4)=0,
解得 a1=-1,a2=-4.
即a的值是-1或-4.
故答案是:-1或-4.
点评 本题考查了一元二次方程的解的定义.能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
18.下列说法中,不正确的是( )
| A. | 同位角相等,两直线平行 | |
| B. | 两直线被第三条直线所截,内错角相等 | |
| C. | 两直线平行,内错角相等 | |
| D. | 同旁内角互补,两直线平行 |
2.设m是方程x2+5x=0的较小的根,n是方程x2+3x+2=0的较小的根,则关于x的一元二次方程x2+mx-n=0的叙述正确的是( )
| A. | 无实根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 不确定 |
19.如果a=2+$\sqrt{3}$,b=$\frac{1}{2-\sqrt{3}}$,那么( )
| A. | a>b | B. | a<b | C. | a=b | D. | a=$\frac{1}{b}$ |
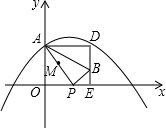 如图,在平面直角坐标系xOy中,抛物线y=ax2+$\frac{5}{6}$x+c过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过点B作x轴的垂线、过点A作y轴的垂线,两直线相交于点D.
如图,在平面直角坐标系xOy中,抛物线y=ax2+$\frac{5}{6}$x+c过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过点B作x轴的垂线、过点A作y轴的垂线,两直线相交于点D.