题目内容
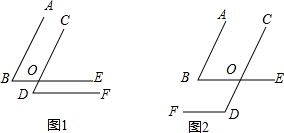
2.如图,∠B、∠D的两边分别平行.(1)如图1,∠B与∠D的数量关系是相等,说明理由.
(2)如图2,∠B与∠D的数量关系是互补,说明理由.
(3)由(1)、(2)用一句话归纳结论如果两个角的两边分别平等,那么这两个角相等或互补.
分析 本题主要利用两直线平行,同位角相等,两直线平行,同旁内角互补及两直线平行内错角相等进行做题.
解答 解:(1)相等;
理由:∵AB∥CD,BE∥DF
∴∠B=∠COE,∠COE=∠D
∴∠B=∠D;
(2)互补;
理由:∵AB∥CD,BE∥DF
∴∠B+∠BOC=180°∠BOC=∠D
∴∠B+∠D=180°.
(3)如果两个角的两边分别平行,那么这两个角相等或互补,
故答案为:相等,互补,如果两个角的两边分别平等,那么这两个角相等或互补.
点评 本题主要考查对平行线的性质的理解和掌握,根据平行线的性质进行证明是解此题的关键.

练习册系列答案
相关题目
12.下列说法错误的是( )
| A. | 无数条直线可交于一点 | |
| B. | 直线的垂线有无数条,但过一点与已知直线垂直的直线只有一条 | |
| C. | 直线的平行线有无数条,但过直线外一点的平行线只有一条 | |
| D. | 互为补角的两个角一个是钝角,一个是锐角 |
10.下列事件中,是不可能事件的是( )
| A. | 打开数学课本使刚好翻到第60页 | |
| B. | 哥哥的年龄一定比弟弟的大 | |
| C. | 在一小时内,你步行可以走50千米 | |
| D. | 经过一个有交通信号灯的路口,遇到绿灯 |
17.下列各式中属于最简二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{12}$ | D. | $\sqrt{0.2}$ |
14.下列各式由左边到右边的变形中,属于分解因式的是( )
| A. | a(x+y)=ax+ay | B. | x2-4x+4=x(x-4+$\frac{4}{x}$) | ||
| C. | 10x2-5x=5x(2x-1) | D. | x2-16+3x=(x+4)(x-4)+3x |
12.已知点A的坐标为(1,3),将线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标为( )
| A. | (3,1) | B. | (3,-1) | C. | (-3,-1) | D. | (1,-3) |
 将一长方形纸片如图所示的方式折叠后,再展开,若∠1=50°,则∠2=65°.
将一长方形纸片如图所示的方式折叠后,再展开,若∠1=50°,则∠2=65°. 某舞台的上方共挂有a,b,c,d四个照明灯,当只有一个照明灯亮时,一棵道具树和小玲在照明灯光下的影子如图所示,则亮的照明灯是( )
某舞台的上方共挂有a,b,c,d四个照明灯,当只有一个照明灯亮时,一棵道具树和小玲在照明灯光下的影子如图所示,则亮的照明灯是( )