题目内容
13．计算下列各式．（Ⅰ）（$\sqrt{3}$-$\sqrt{2}$）（4$\sqrt{\frac{1}{2}}$+$\sqrt{3}$）-$\sqrt{6}$；
（Ⅱ）（a$\sqrt{8a}$+$\sqrt{32{a}^{3}}$）÷$\sqrt{2a}$．
分析 （1）先化简二次根式，再根据乘法分配律去括号，最后合并可得；
（2）先化简二次根式，再合并括号内同类二次根式，最后计算除法即可得．
解答 解：（Ⅰ）原式=（$\sqrt{3}$-$\sqrt{2}$）（2$\sqrt{2}$+$\sqrt{3}$）-$\sqrt{6}$
=2$\sqrt{2}$×$\sqrt{3}$+（$\sqrt{3}$）2-2$\sqrt{2}$×$\sqrt{2}$-$\sqrt{2}$×$\sqrt{3}$-$\sqrt{6}$
=2$\sqrt{6}$+3-4-$\sqrt{6}$-$\sqrt{6}$
=-1；
（Ⅱ）原式=（2$\sqrt{2}$a•$\sqrt{a}$+4$\sqrt{2}$a•$\sqrt{a}$）÷$\sqrt{2a}$
=6$\sqrt{2}$a•$\sqrt{a}$÷（$\sqrt{2}$•$\sqrt{a}$）
=6a．
点评 本题主要考查二次根式的混合运算，熟练掌握二次根式混合运算顺序及其运算法则是关键．
练习册系列答案
相关题目
4．下列大小关系中，正确的是（ ）
| A． | $-100\frac{1}{3}＜-101$ | B． | -100＜-101 | C． | $-100＞-100\frac{1}{3}$ | D． | $-100\frac{1}{3}＞-100$ |
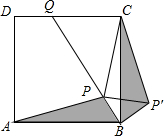如图，点P是正方形ABCD内一点，点P到点A，B和C的距离分别为$\sqrt{10}$，1，2$\sqrt{2}$，△ABP绕点B旋转至△CBP′，连结PP′，并延长BP与DC相交于点Q，则∠CPQ的大小为45（度）
如图，在Rt△ABC中，∠B=90°，AC=120cm，∠C=30°，点D从点C出发沿CA方向以8cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以4cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t 秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．
3．如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（3，1），（3，0），（3，-1）…根据这个规律探索可得，第20个点的坐标为（ ）
| A． | （6，0） | B． | （6，-1） | C． | （6，1） | D． | （6，2） |