题目内容
如图，正方形DEFG内接于Rt△ABC，∠C=90°，AE=4，BF=9，则tanA=考点：相似三角形的判定与性质,锐角三角函数的定义
专题：
分析：根据条件可证明△ADE∽△GFB，利用相似三角形的性质可求得DE，在Rt△ADE中，由正切函数的定义可求得tanA．
解答：解：∵四边形DEFG为正方形，
∴∠DEA=∠GFB=90°，DE=GF，
∵∠C=90°，
∴∠A+∠B=∠A+∠ADE=90°，
∴∠ADE=∠B，
∴△ADE∽△GFB，
∴
=
，即
=
，解得DE=6，
∴tanA=
=
=
，
故答案为：
．
∴∠DEA=∠GFB=90°，DE=GF，
∵∠C=90°，
∴∠A+∠B=∠A+∠ADE=90°，
∴∠ADE=∠B，
∴△ADE∽△GFB，
∴
| AE |
| GF |
| DE |
| BF |
| 4 |
| DE |
| DE |
| 9 |
∴tanA=
| DE |
| AE |
| 6 |
| 4 |
| 3 |
| 2 |
故答案为：
| 3 |
| 2 |
点评：本题主要考查相似三角形的判定和性质，由条件证明三角形相似求得DE的长是解题的关键．
练习册系列答案
相关题目
如图，共有12个大小相同的小正方形，其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分，先从其余的小正方形中任取一个涂上阴影，则能构成这个正方体的表面展开图的共有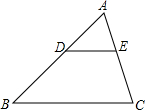
如图，在△ABC中，DE∥BC，DE与边AB相交于点D，与边AC相交于点E，如果AD=3，BD=4，AE=2，那么AC=